| SOLSTICE: An Electronic Journal of Geography and Mathematics. (Major articles are refereed; full electronic archives available) |
 |

Sandra Lach Arlinghaus
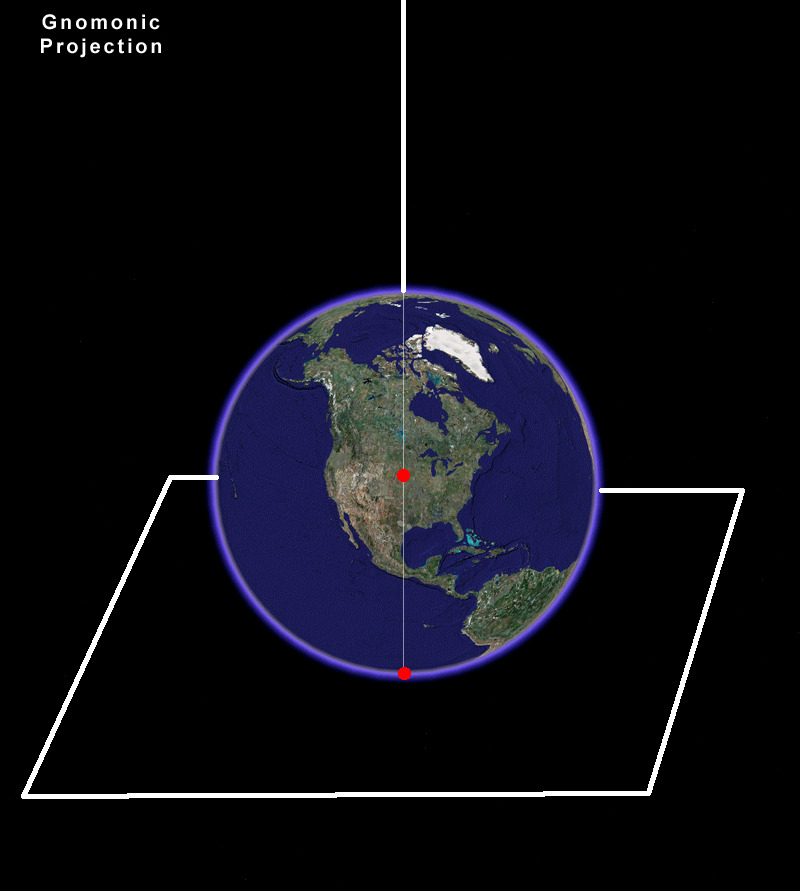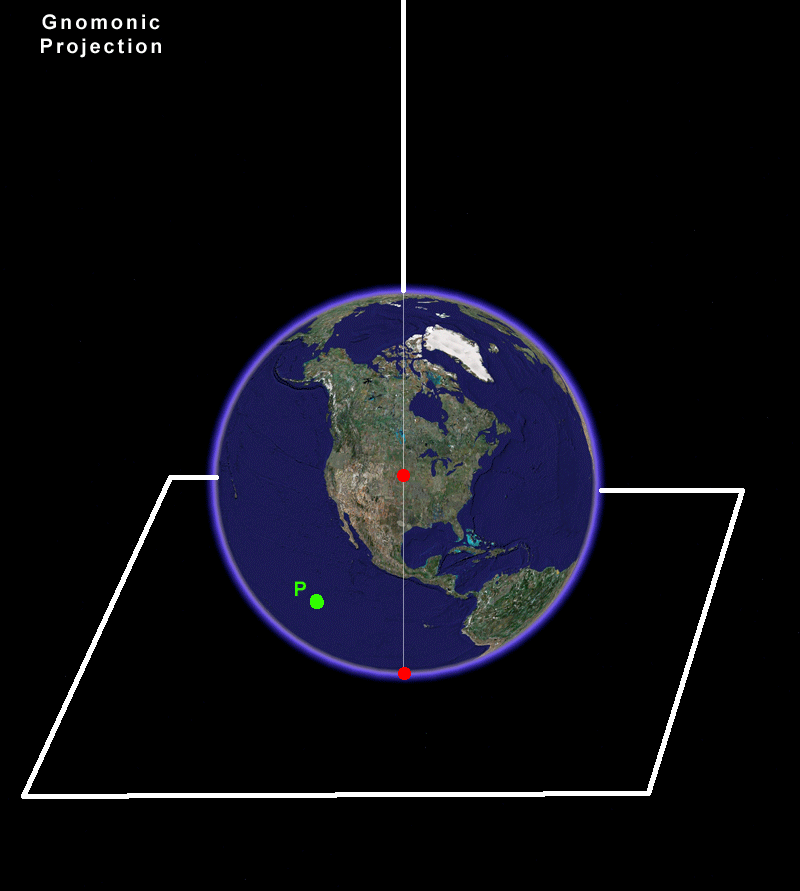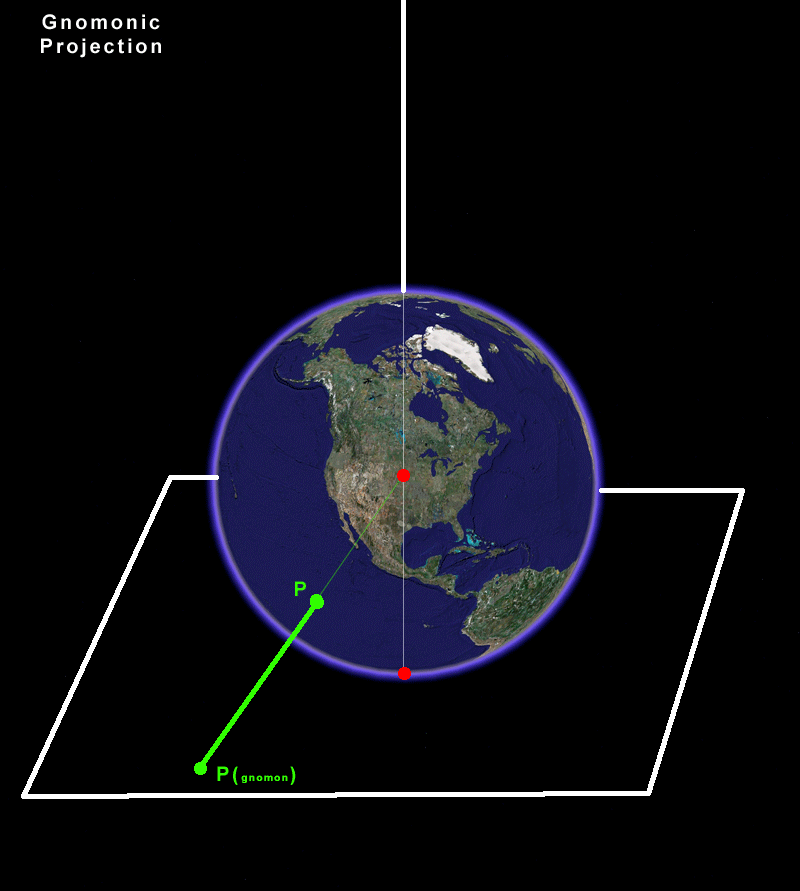
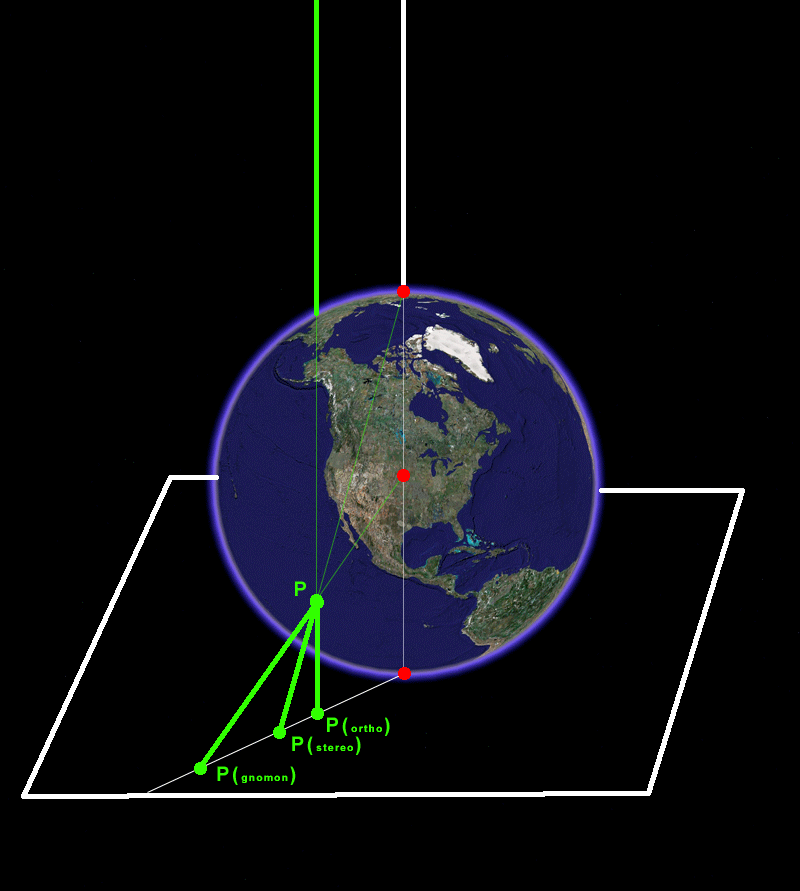
Benoit Mandelbrot has shown us the power of computer-generated images to make mathematical concepts come alive that had otherwise been tucked away in mathematics classrooms [Mandelbrot, 1982]. What is accurate in terms of definition/proof presentation may not penetrate the minds of those less gifted in mastering the mathematical notation and its underlying system of logic. Beautiful images, conceived by those who understand both the abstract concepts and their representation using current technological capability, can go a long way toward making heretofore inaccessible concepts become accessible.
A recent example of such transformation in accessibilty appeared in YouTube this past summer [Arnold and Rogers, 2007]. Imagine being able to see Möbius transformations come alive as an animated sequence showing their relations to each other in the plane and then, unifying those representations by lifting them into the third dimension on a sphere. Take a look at this award-winning work, now. Use the link above to view it at low resolution on YouTube. Original Source Douglas N. Arnold and Jonathan Rogness, June 2007: http://www.youtube.com/watch?v=JX3VmDgiFnY