Institute of Mathematical Geography

SOLSTICE:
An Electronic Journal of
Geography and Mathematics.
(Major articles are refereed;
full electronic archives available)

THE ANIMATED PASCAL
Sandra Lach Arlinghaus

There are a number of elegant theorems about conics in the projective plane. The animations below illustrate a few associated constructions.

Figure 1 shows an animated illustration of Pascal's Theorem:

PASCAL'S THEOREM [Coxeter, 1961]: If A, B, C, A', B', C' are six vertices of a hexagon inscribed in a conic, then the points of intersection of opposite sides of the hexagon, L, M, and N, are collinear (lying along line z).

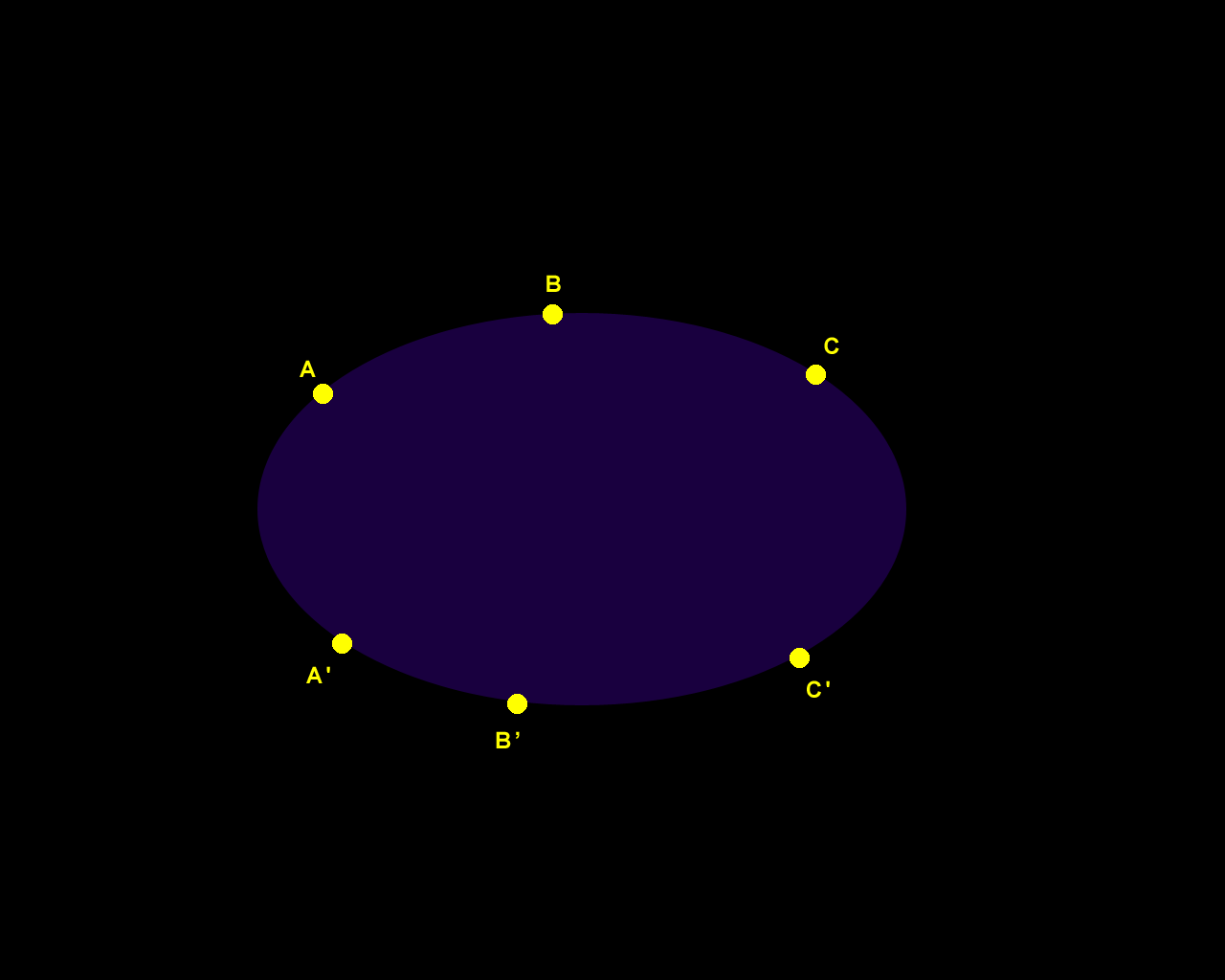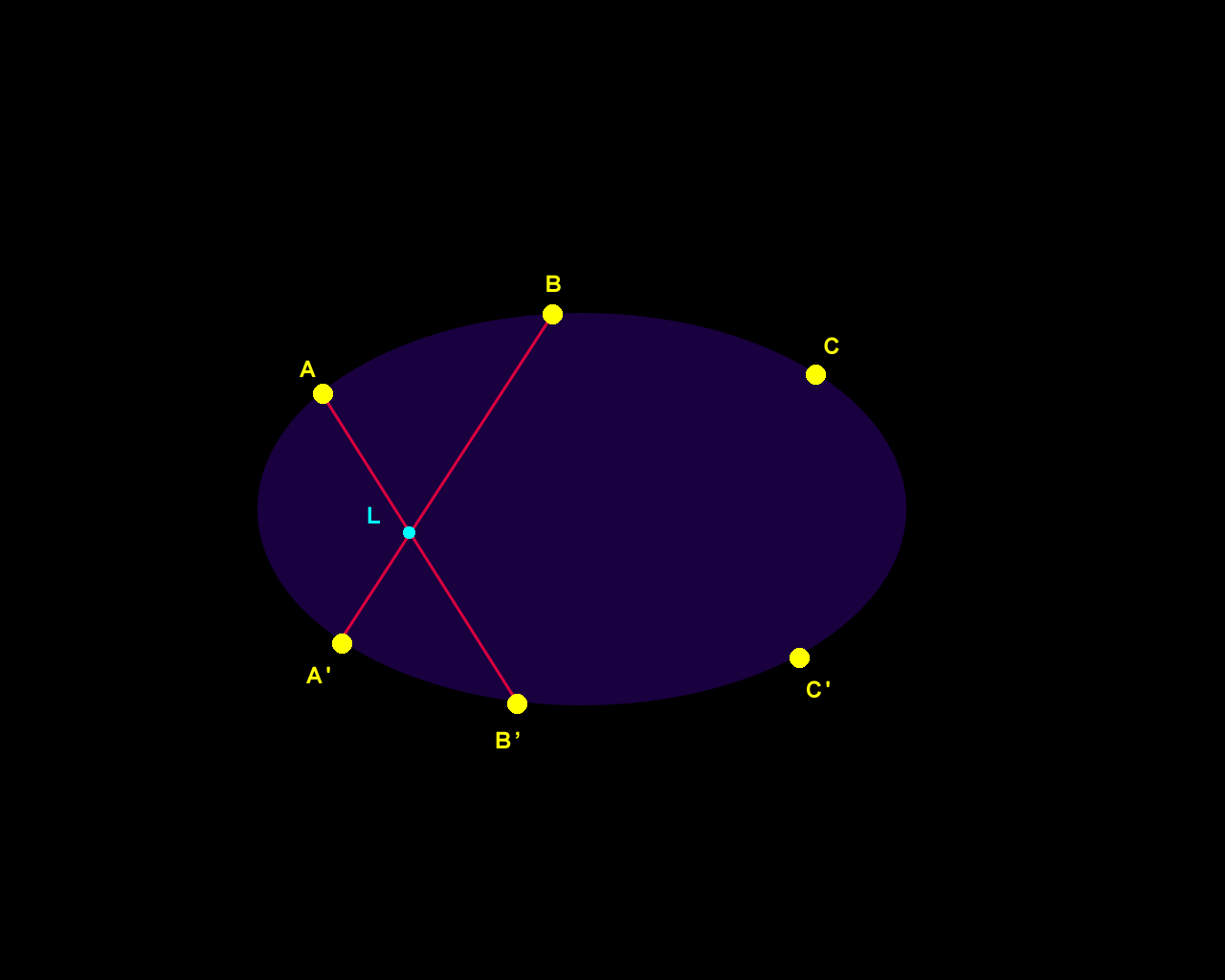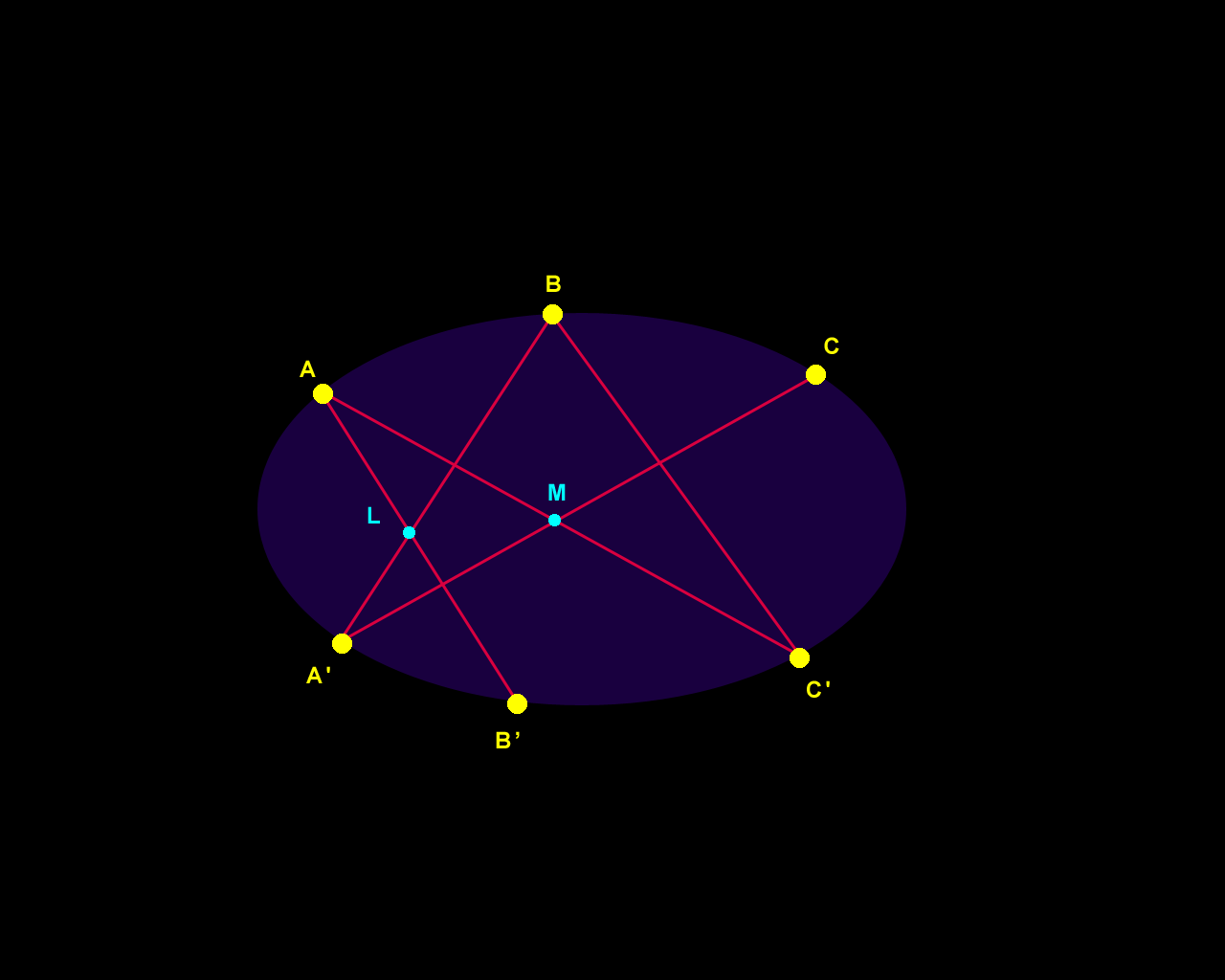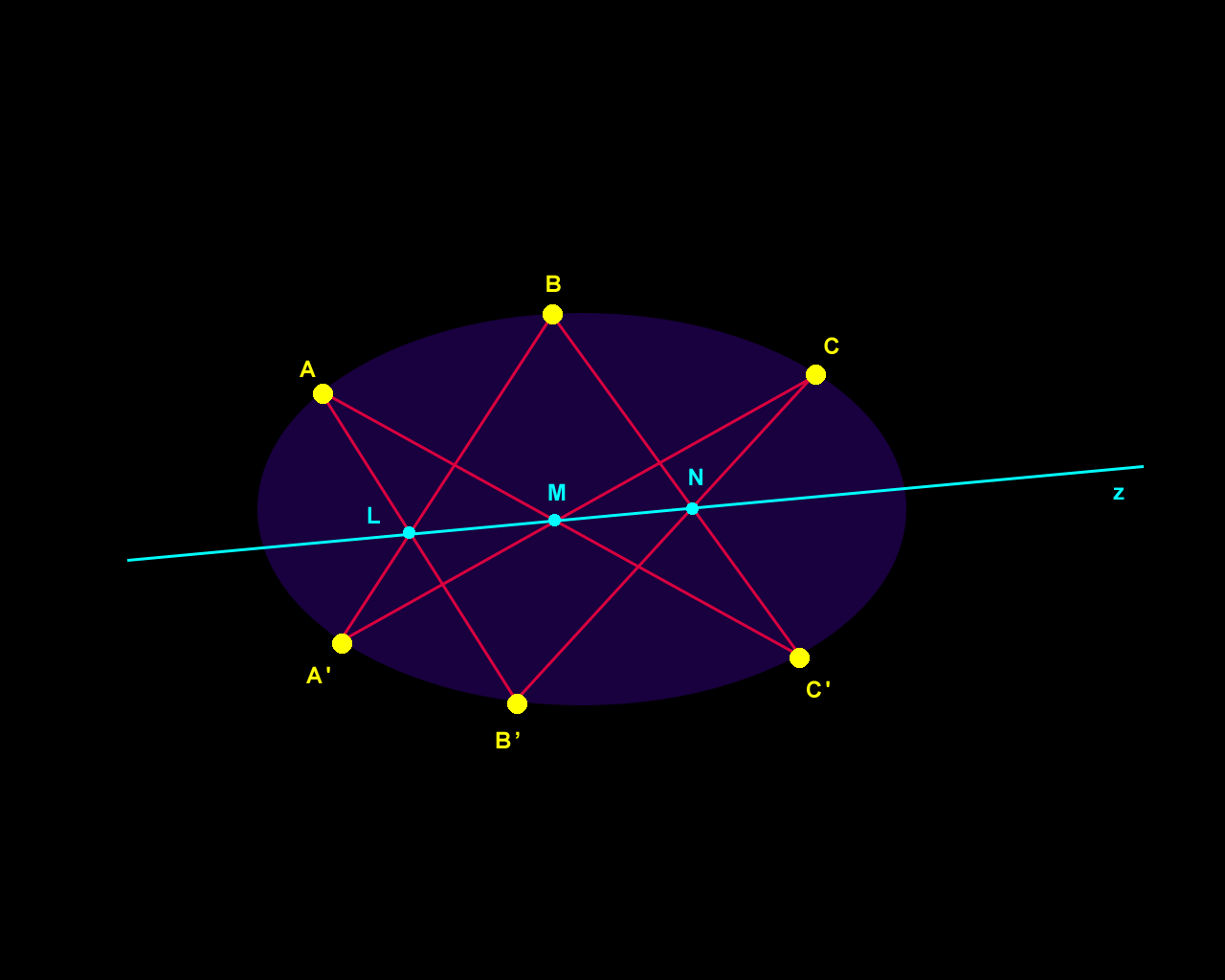Figure 1. Pascal's Theorem.

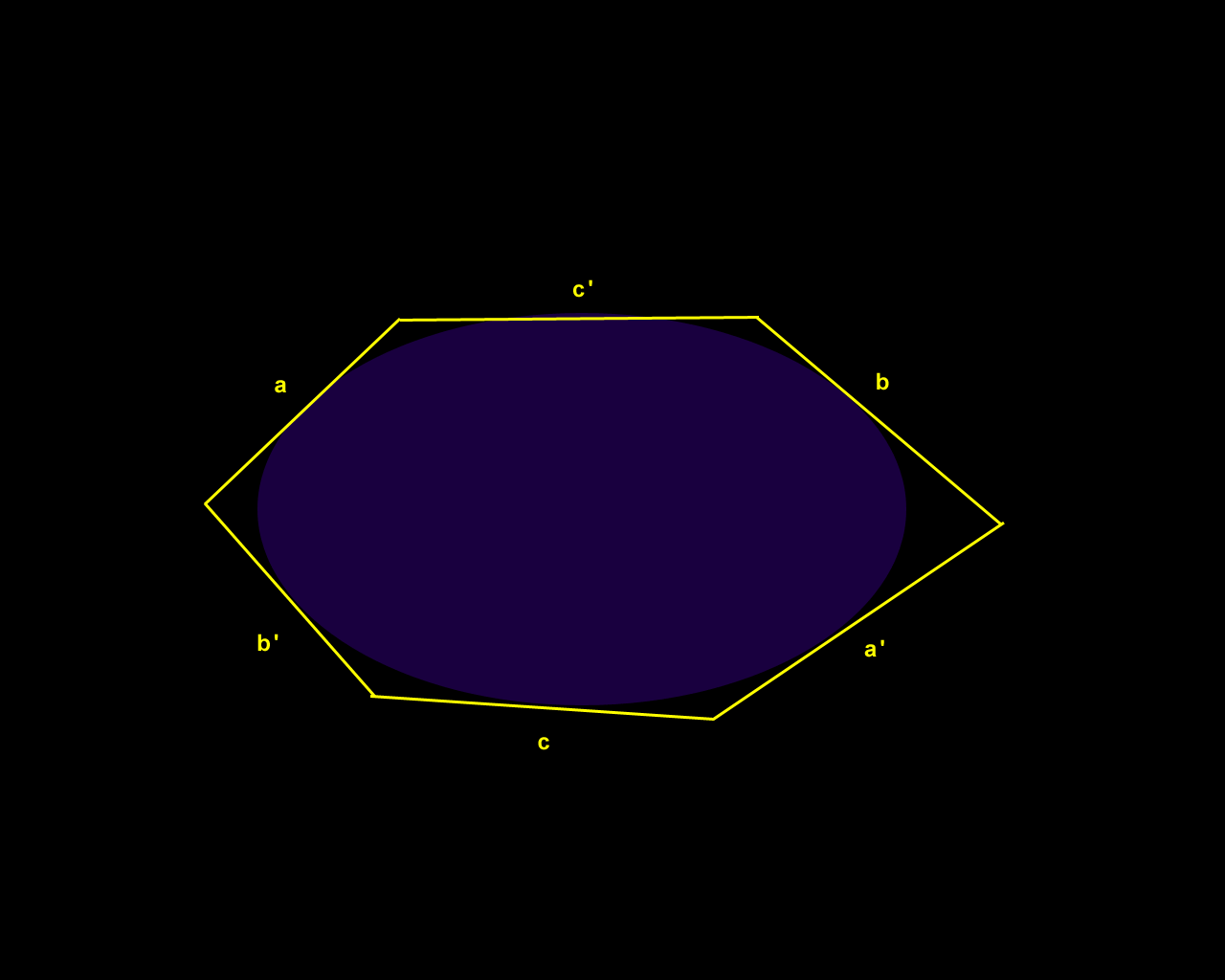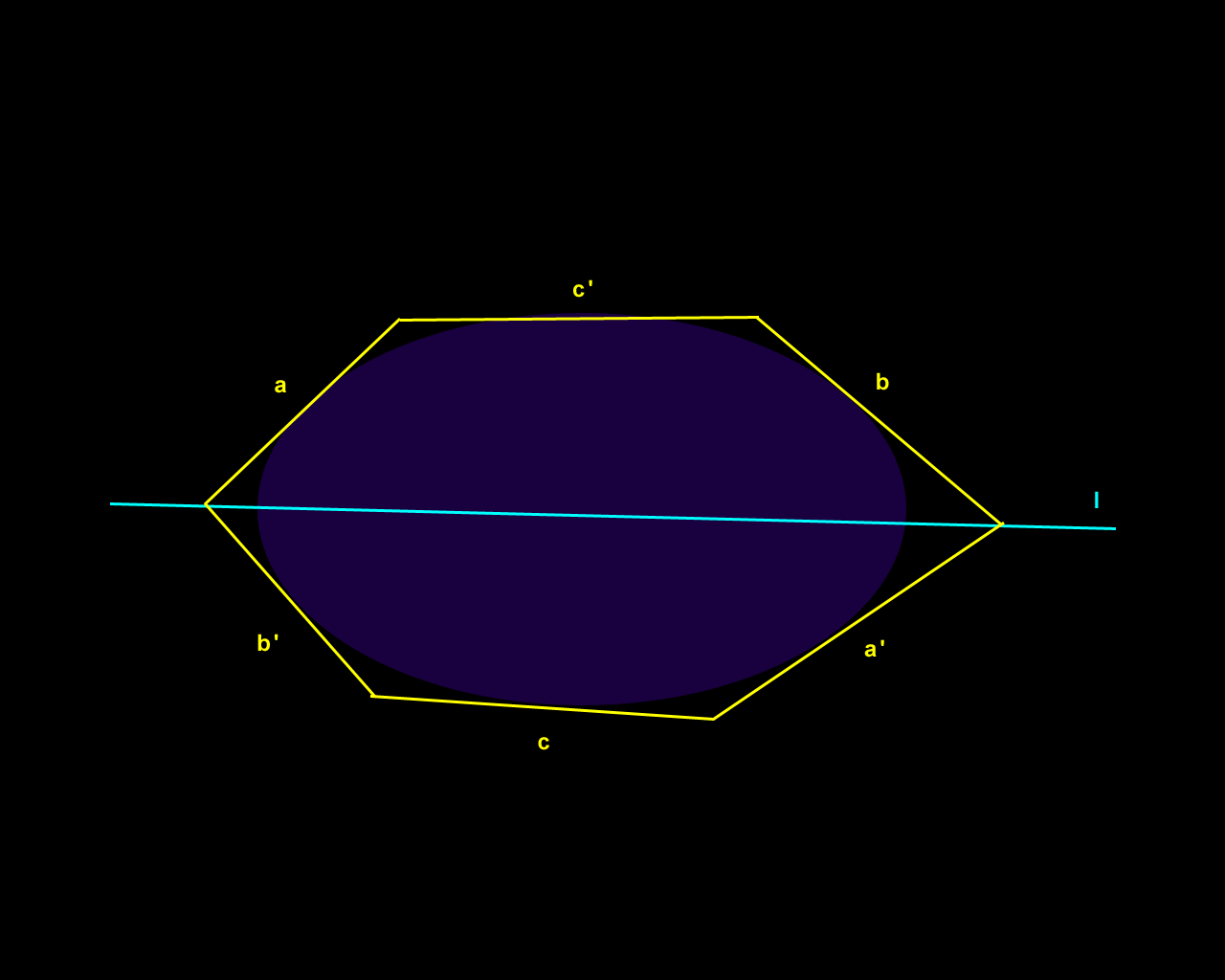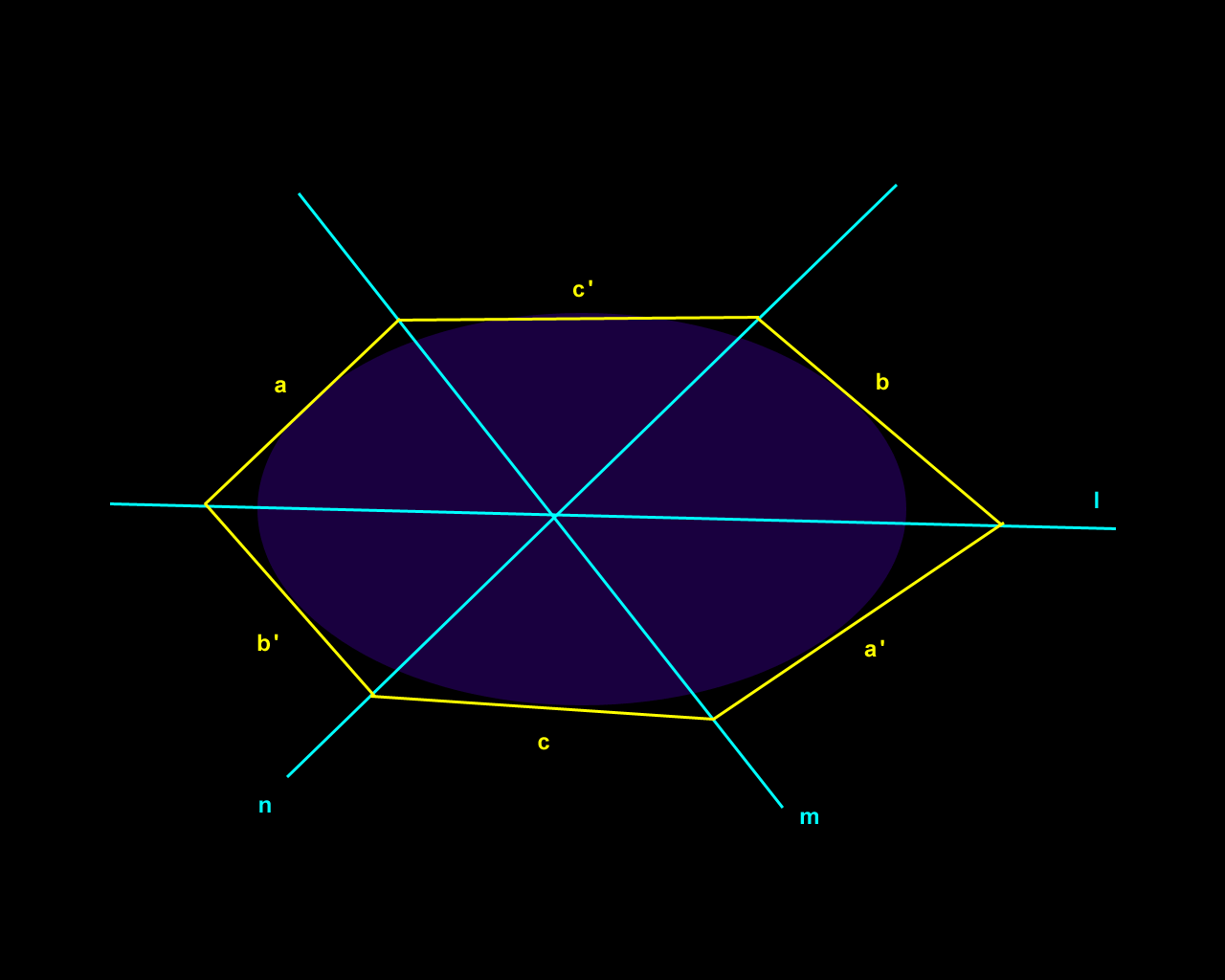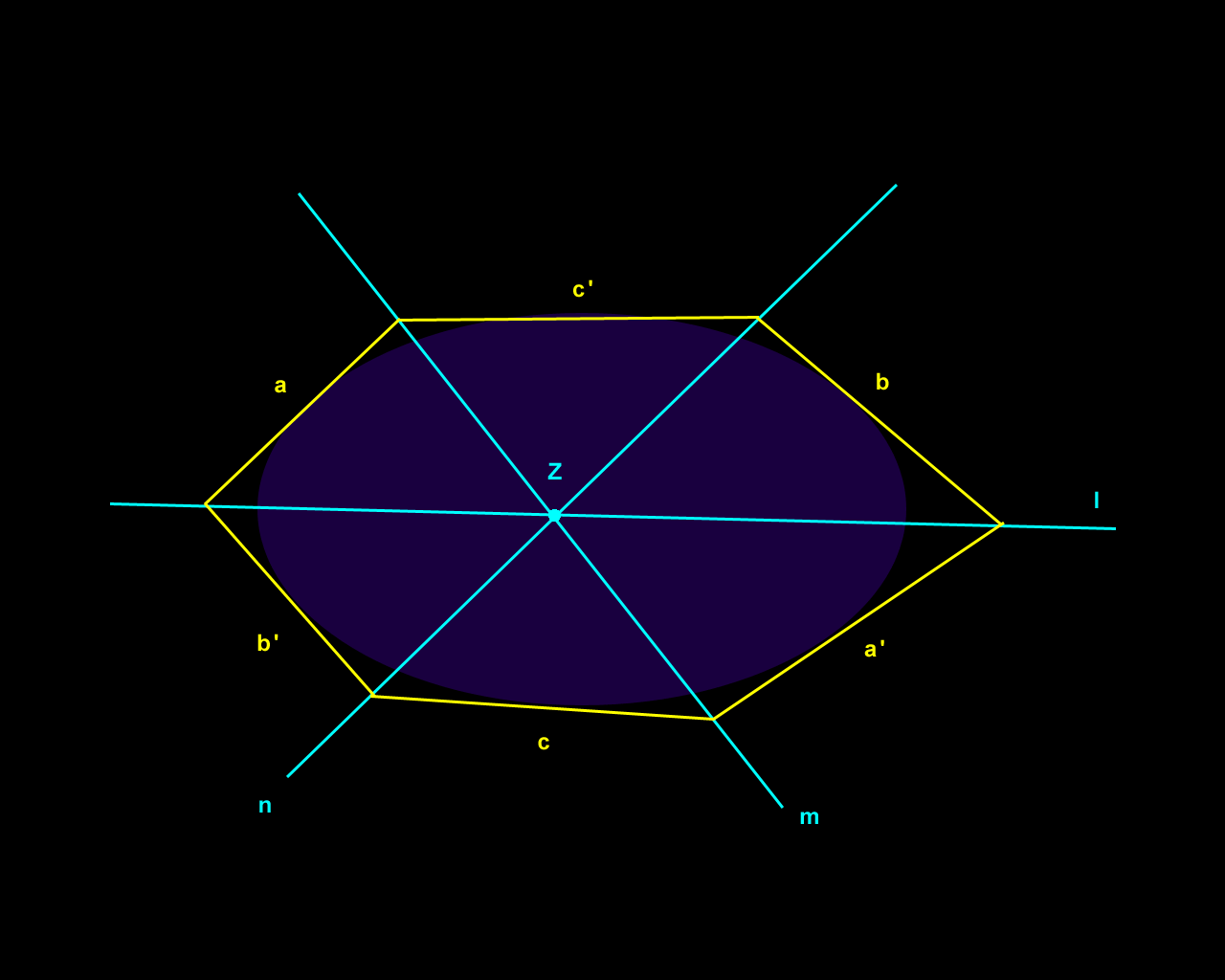Figure 2 shows an animated illustration of the dual of Pascal's Theorem:

BRIANCHON'S THEOREM [Coxeter, 1961]: If a, b, c, a', b', c' are six sides of a hexagon circumscribed about a conic, then the lines joining opposite vertices (the diagonals) of the hexagon, l, m, and n, are concurrent (at the point Z).

Figure 2. Brianchon's Theorem: dual of Pascal's Theorem.

Figure 3 shows an animated illustration of the converse of Pascal's Theorem used to create a specific, important construction:

BRAIKENRIDGE-MACLAURIN CONSTRUCTION [Coxeter, 1961]: Construction of a conic through 5 given points based on:

Fiugre 3a. This construction is the converse of Pascal's Theorem. Choose line z through L, leading to point C' on the conic through the 5 given points, A, B, C, A', B'.

Figure 3b. This construction is independent of the choice of z. Choose a different line line z through N. It, too, will produce a point C' in a location different from that of Figure 3a but the new C' will also lie on the conic through the 5 given points!

Part of the motivation for creating these animations lies in offering helpful graphics to illuminate notation. Another part of it is to build a foundation on which to continue ongoing research linking non-Euclidean geometries and the compression of (geo)graphics [Arlinghaus and Batty, 2005] -- within the digital world but perhaps not beyond the "limits" of the Escher series! [Escher, Circle Limit series; kmz file link).

Click to download Google Earth KMZ file

References:

Arlinghaus, S. L. and Batty, M. "Zipf's Hyperboloid?" Solstice: An Electronic Journal of Geography and Mathematics, Vol. XVII, No. 1. Institute of Mathematical Geography, http://www.imagenet.org/
Coxeter, H. S. M. 1961. Introduction to Geometry. New York: John Wiley & Sons. 252-254.
Escher, M. C. 1956. http://en.wikipedia.org/wiki/M._C._Escher

Solstice was a Pirelli INTERNETional Award Semi-Finalist, 2001 (top 80 out of over 1000 entries worldwide)

One article in Solstice was a Pirelli INTERNETional Award Semi-Finalist, 2003 (Spatial Synthesis Sampler).

Solstice is listed in the Directory of Open Access Journals maintained by the University of Lund where it is maintained as a "searchable" journal.

Solstice is listed on the journals section of the website of the American Mathematical Society, http://www.ams.org/

Solstice is listed in Geoscience e-Journals

Solstice is listed in the EBSCO database.

IMaGe is listed on the website of the Numerical Cartography Lab of The Ohio State University: http://ncl.sbs.ohio-state.edu/4_homes.html

Congratulations to all Solstice contributors.

Solstice: An Electronic Journal of Geography and Mathematics,
Volume XVIII, Number 2
Institute of Mathematical Geography (IMaGe).
All rights reserved worldwide, by IMaGe and by the authors.
Please contact an appropriate party concerning citation of this article: sarhaus@umich.edu
http://www.imagenet.org

1964 Boulder Drive,
Ann Arbor, MI 48104734.975.0246
image@imagenet.org