| SOLSTICE: An Electronic Journal of Geography and Mathematics. (Major articles are refereed; full electronic archives available) |
 |
| SOLSTICE: An Electronic Journal of Geography and Mathematics. (Major articles are refereed; full electronic archives available) |
 |
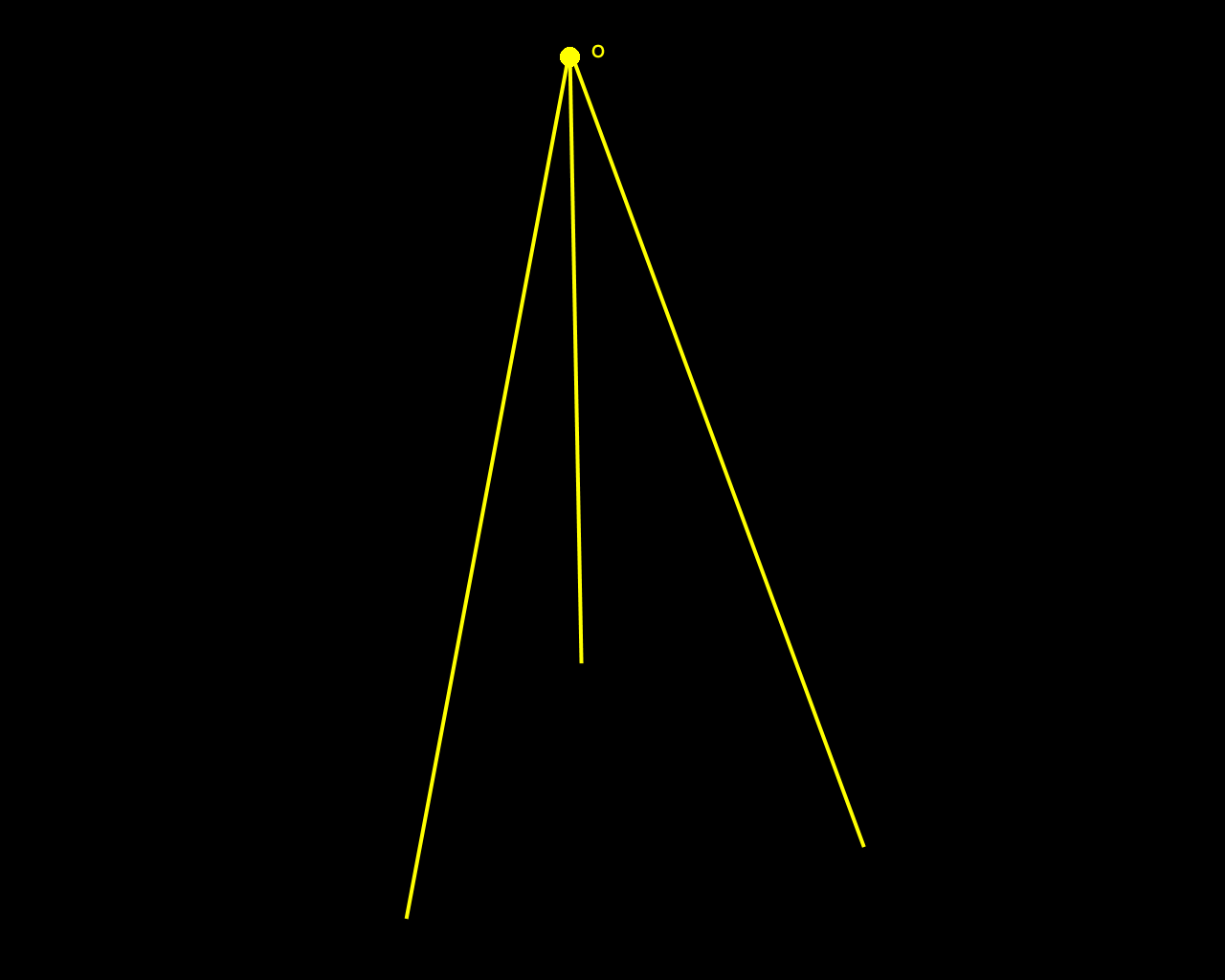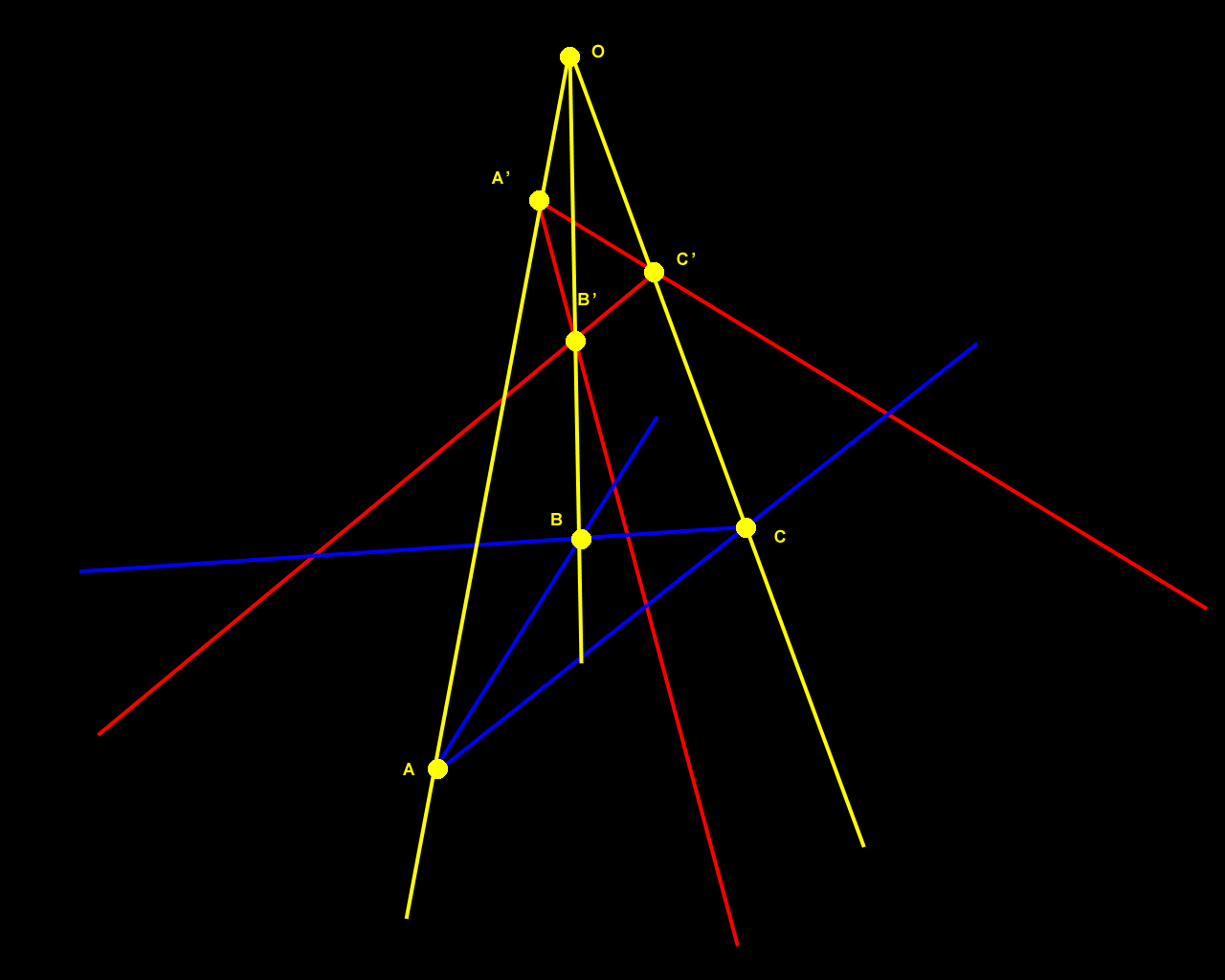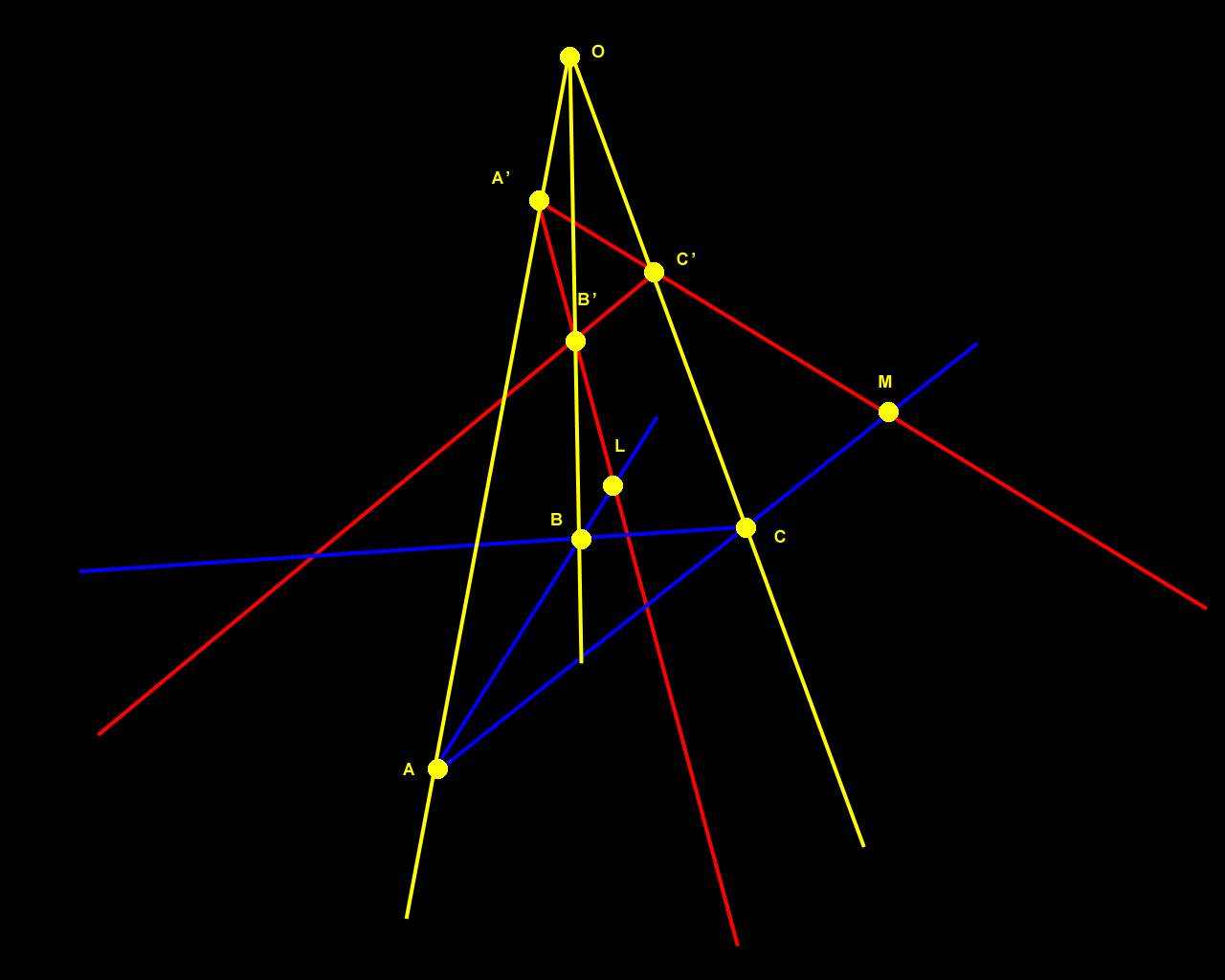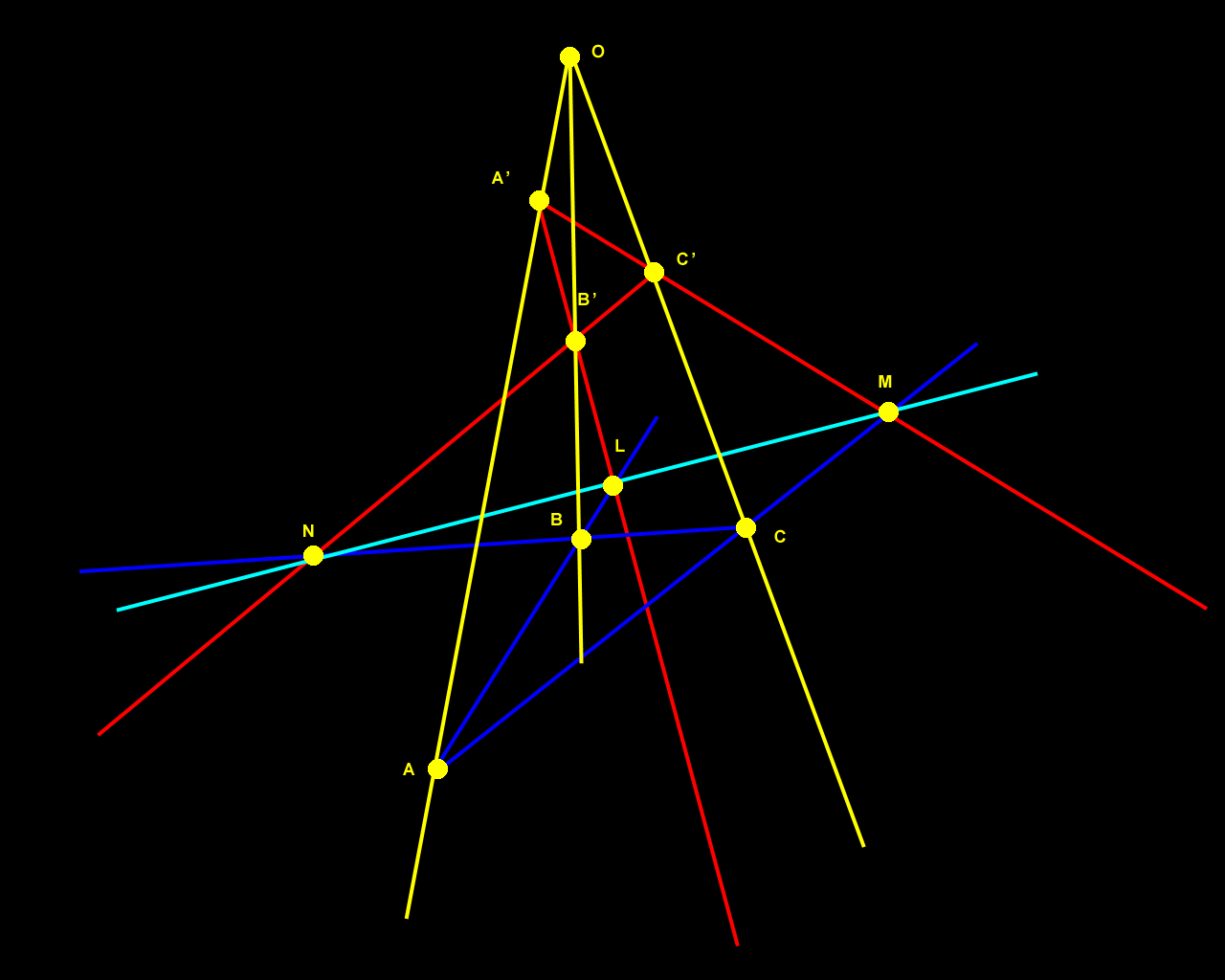 Figure 1. Desargues's Two-Triangle Theorem visualized in the plane. |

Solstice:
An Electronic Journal of Geography and Mathematics,
|