
Source of original map |
Source of original map: |
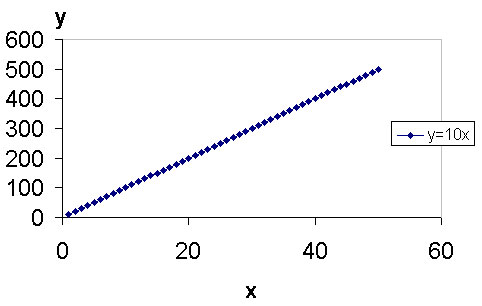
y=10x
 |
 |
An earlier article in Solstice examined the merits of an animated sequence of Triangulated Irregular Networks (TINs) to introduce an element of order into complicated pattern. In that earlier map (takes time to load on a slow modem), the time distance between successive frames was constant (12/100 of a second between successive frames in the set of 50 frames "in" and 50 frames "out"). Views such as this offer a way to clarify geographic ideas. They might also be used, however, to make mathematical concepts come alive.
It is this latter idea that is examined here. When a constant
interval is chosen between successive animation frames, a linear equation
is portrayed: in this case, for ease in generalization, suppose y=10x
--- the time-spacing between successive frames ("in" only) is 10/100 of
a second. The left column in the table below shows half of the map
from the previous article along with the graph it might be viewed to represent.
Unit changes in x values produce a constant difference between corresponding
y values: the viewer is set down on Earth at an apparently uniform
rate.

Source of original map |
Source of original map: |
y=10x
 |
 |
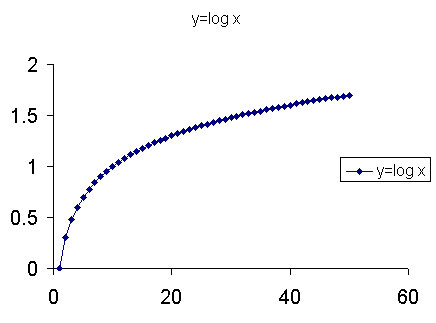
Suppose instead of using y=10x, one "mapped" y=log10 x. The results would appear as in the right hand column of the table above. As values of x get larger, the successive differences between the corresponding values of y get smaller. Hence, the viewer is "smashed" more rapidly to Earth!
This procedure need not be limited to continuous functions. The sequence of maps appears continuous but is in fact discrete. Animaps can easily be used as well to model discrete series.
What can be used in one direction to shed light on geographic ideas
can be turned around to make possibly difficult mathematical ideas more
appealing to learn. This sort of idea is just a beginning--the reader
might try numerous other interesting variations on this theme.