 Direct e-mail to the author:
click here or send to nystuen@umich.edu
Direct e-mail to the author:
click here or send to nystuen@umich.eduWhy Whales Don't Freeze or Kidney-Shaped Airports:
Spatial Analysis and Spatial Design.
John D. Nystuen
University of Michigan
 Direct e-mail to the author:
click here or send to nystuen@umich.edu
Direct e-mail to the author:
click here or send to nystuen@umich.edu
Paper Presented at
the Association of American Geographers Annual Meeting
Fort Worth, Texas
April 2, 1997
KEYWORDS: boundary flows, spatial analysis, spatial design.
Abstract
Whales are warm bodies in a cold sea. Heat flow is a function of temperature gradient and, given long exposure and the large temperature difference between the interior of the whale's body and its watery environment (even with very good insulation), it seems as though whales should freeze. The arrangement of the blood vessels near the surface of the whale's skin creates a counter-current action that prevents this outcome. Kidneys contain similar counter-current processes that perm it concentration and transfer of waste products from blood vessels to urine tract. The shape of the kidney is an important feature in this process. An airport is a transfer point between travel domains in which two unlike carriers, motor vehicles and airplanes, must interact to exchange people and luggage. The exchange is facilitated by kidney-shaped airports. These unlike phenomena share some fundamental spatial properties, which when acknowledged, provide understanding and opportunity for design. Do airports have to be kidney-shaped? Certainly they do not, but it helps if they are. Spatial analysis addresses the spatial/temporal context in which things happen, an approach that has proven to be very useful for understanding spatial processes and for contributing to the design of effective spatial systems. Geographers have learned much through spatial analysis but have been little concerned with spatial design. Planners and architects focus on spatial design but often without addressing underlying spatial properties. The advent of GIS refocuses attention on fundamental spatial properties; geographers can play a pivotal role in this now interdisciplinary endeavor.
Introduction
My interest in boundaries and boundary processes led me to consider how the shape of boundaries facilitates or hinders exchange across boundaries (Nystuen, 1967). Today, I will share with you, in this oddly titled talk, some examples of very unlike boundary processes that are influenced by passive shapes, indeed, are made possible by the pattern of the flow channels near or in the boundary. In recent years geographers have shied away from analogies about spatial systems drawn from other disciplines particularly condemning biological analogies or metaphors as a means for understanding geographical systems. I think that stricture stifles imagination and limits opportunity for discovery. I have learned much from such comparisons. Also not to be discounted is the pleasure found in making connections between unlike phenomena. Let me describe the connection between whales, kidneys, and kidney-shaped airports.
Why Whales Don't Freeze
Whales are warm bodies in a cold sea. They are mammals with an internal body temperature close to that of human beings yet they spend much of their time in oceans that are at near freezing temperatures. Whales commonly maintain a temperature gradient close to 35 degrees Celsius (63 degrees Fahrenheit) in a distance of a meter or less from their warm interior to their cold watery environment. Heat flows down a temperature gradient and, even with thick blubber as insulation, over time a disastrous heat loss might be expected. Whales are not likely to be able to eat fast enough to generate a balance for the heat loss; for one thing, the food itself must be warmed up after being eaten. Heat exchange for three dimensional bodies is proportional to the surface area of contact. Even though this area is minimized by the rounded shape of the whale, it is still vast. The total calorie exchange would appear to be vast. At first consideration then, it seems that whales should freeze to death.
They avoid this fate by the arrangement of the blood vessels near the surface of their skins. These vessels are shaped like hairpins pointed directly outward with the sharp turn next to the surface of the skin. Consider the temperature of the blood just at the turn near the skin surface (Figure 1). It is cool due to the proximity of the cold sea. As the blood returns to the interior of the whale it is warmed by heat flow from its warmer surroundings. Part of those surroundings is the set of blood vessels carrying blood on the outward leg of the hairpin route. The out-bound blood loses heat to the cooler in-bound blood, which in turn is warmed. By the time the outbound blood reaches the hairpin turn it is as cold as the sea itself. By the time the in-bound blood reaches the interior of the whale, it is as warm as the interior. There is very little temperature gradient between the whale's surface and the sea, ergo, there is very little heat transfer, for a temperature gradient is needed to transfer heat.
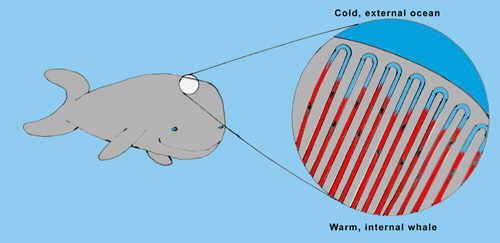
Figure 1. The whale's counter-current boundary system.
The counter-current arrangement maintains a large heat gradient without the need for a heat pump such as is found in a refrigerator. Energy is required to move the blood. The countercurrent system will not work without motion in the blood stream. Of course, if the whale's heart stops beating, heat loss to its environment is the least of its problems. The passive counter-current shape is found in several natural and man-made mechanisms. The blue heron standing in icy water keeps the heat from draining out of his body through his feet, in part, by standing on one foot, but also by the counter-current design of blood vessels in its other leg. The foot that is in the water is cold but heron's body remains warm. Engineers are familiar with this design and use it to maintain high temperatures inside boilers without having the boiler sides very hot and without much heat loss to the atmosphere surrounding the boiler. The design is particularly useful for nuclear reactors for they get very hot inside. The design requires that the coolant keep moving.
In the abstract, the high energy gradient is possible because of the shape of the semi-permeable transportation routes near the boundary of the two media. In this case, these routes are permeable to heat flow. No heat pump is required to move heat from the cold media to the hot as in a refrigerator. The only energy required is that needed to drive the fluid through the transportation channels.
The Kidney
Another biological example of the counter-current pattern is found in the kidney. Here the problem is to concentrate sodium ions and other salts in the urine by transferring these ions from the blood stream to the urine tract while maintaining the proper water-salt balance in the body: also by expelling or conserving water as the need may be. This transfer is accomplished in the kidney. The function of certain details of the anatomy (read morphology in geographer's parlance) has only been established in recent decades. One mystery was the purpose of the Loops of Henle. These are long hairpin-shaped loops in the urine ducts within the kidney pointing from the outside or cortex of the kidney toward the medulla or concave inner core of the kidney (Figure 2). The blood vessels of the kidney loop into the medulla in the same fashion -- by making long hairpin turns. Sodium ions and other ions move through the semi-permeable wall of the blood vessels into the intercellular zone near the urine ducts and thence into the urine ducts by osmotic pressure. Ions move down the density gradient. The counter-current process operates along the Loops of Henle such that high concentrations of salts are possible at the turn of the loops. This is because blood approaching this area builds up high ion concentrations but looses the concentration via the counter-current action on the out-bound leg of the blood vessel. The site of active transport of sodium ions is along the length of the ascending limb of the Henle's loop (Mercer and Wasserman). In this fashion high concentrations of uric acid and salts are possible in the urine of land animals. A passive energy gradient is maintained by the shape or arrangement of these loops and the system satisfies one requirement our bodies must meet in order to stay out of the salty sea from whence we came.
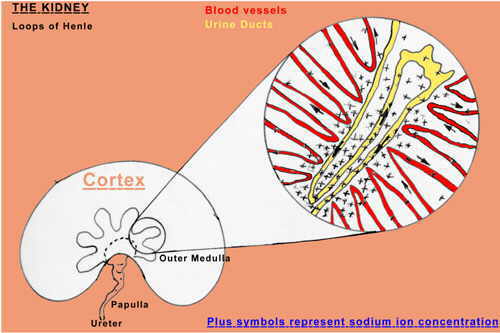
Figure 2. Simplified schematic of the kidney.
The operation of the kidney is very intricate and more complicated than I indicate here. Suffice to note that the arrangement of the transportation channels permits a transfer of an element from one medium to another. The kidney example is the reverse of the whale example. In the case of the whale, the purpose of the shape is to prevent heat transfer between two media. In the case of the kidney the purpose is to sustain a transfer at high concentrations.
Because the walls of the transfer channels are semi-permeable, ions can be exchanged whenever channels are in close proximity. This explains the kidney shape. Transfers occur along Henle's loops. Salt concentrations fall in all direct ions from this zone. The counter-current action in the blood vessels ceases by the fanning out or spreading of the blood vessels in the cortex of the kidney. The urine ducts loop back to the outer medulla thereby lowering the ionic pressure and then return to the concentrated zone increasing the ion pressure and exiting from the kidney into the ureter at the concave inner surface of the kidney. The length of the Henle's loops determines the maximum concentration that can be achieved. Desert animals have long loops. Blood travels at near constant speed through the vessels. The speed of water flow in the urine ducts is a variable and regulates the degree of uric acid concentration. The kidney is a marvelous organ and, as I said before, much more complicated than I describe here. However, we can learn a lesson from its shape.
Kidney-Shaped Airports
The kidney has an efficient shape for its purpose -- to transfer elements from one medium to another. The shape is an interesting form at various geographic sales. We are often concerned with the transfer of elements from one travel domain to another. For example, from airplanes to automobiles at airport terminals. At an airport the stream of airplanes and the stream of surface vehicles are best kept separate. Normally the transportation routes (spatial domains) of the two types of vehicles do not cross for, if they do, extra effort and expense must be used for traffic control or for building structures such as bridges or tunnels to eliminate grade crossings. Each type of vehicle has its own movement characteristics. Most airplanes are much larger than cars and must have considerable head and shoulder room to safely maneuver when on the ground. They land at high speed on linear runways and then slow down and taxi to the terminals. Motor vehicles ap proach the terminal in a similar fashion, reducing velocities from open highway speed to maneuver into position at the terminal but they are not as large a space user as taxiing aircraft. Both aircraft and motor vehicles are concentrated around the terminal building. The elements of exchange are, of course, people, luggage and cargo. Many huge airports have radial walkways leading to the departure gates from the center of the terminal building. People are concentrated at the terminals and fan out to board and leave by plane, When arriving by air, they leave the terminal by motor vehicle on a concave transport route at the inner surface of the terminal building. Basically, transportation carriers with different spatial travel domain are required to interact with some sort of preservation of the elements exchanged; that is, what comes in must also leave otherwise people and things will pile up in the terminal. An efficient design is to have the domain of the carrier with the larger space needs wrapped around the domain of the carrier with fewer space needs. The whole thing is kidney-shaped.
Many medium and large airports are, in fact, this shape. O'Hare Airport in Chicago is a perfect example (Figure 3. Chicago's O'Hare). Most likely if you consider the metropolitan airport nearest your home you will discover it is some version of this basic shape. Airport terminals can be classified into three types by shape or layout: linear, kidney-shaped, and compound. Terminals for small airports are usually linear in form. They reflect the need for only a single linear runway for the airplanes. For medium-sized airports, with more than one runway involved (each oriented in different direction) there is some advantage in placing terminals near the intersection of the runways. This defines a concave space for the approach road and the beginnings of the kidney shape. For very large international terminals, traffic is sufficiently great to justify intermediate transportation domains linking motor vehicles and aircraft. The problem with the large terminals is that the walking link becomes inconveniently long. People who frequently use O'Hare Airport or the Miami Airport probably understand this problem. Other examples of kidney-shaped airports are La Guardia and Newark in the New York Region; San Francisco's International Airport; and, Tokyo's Narita International Airport. Underground light or heavy rail connectors or full circle terminals such as Kennedy Airport in New York in which surface transportation paths cross aircraft paths via bridges for aircraft or tunnels for surface vehicles may be utilized. These large terminals may take a variety of forms but they are no longer planar: that is, paths on a two dimensional surface where unlike paths do not cross (Arlinghaus and Nystuen). The Seattle-Tacoma Airport is an example of a kidney shaped airport with outliers connected by underground light rail vehicles. One common pattern of a non-planar system is comb-like with a straight main stem and shorter perpendicular arms where the departure gates are located. The new Denver and the new Atlanta airport are examples of compound designs as is the Dallas-Fort Worth Airport. This arrangement comes with the added expense and inconvenience of an intermediary transportation mode between the highway vehicles and the aircraft. If that mode is a heavy rail, such as a short subway, it works best if its track is linear, hence the comb or marina-like pattern. Such airports require huge land area and are often found far from the metropolitan core.

Figure 3. Chicago, O'íHare International Airport.
Travel effort always involves three types of costs: acceleration, uncertainty, and queuing. Acceleration is associated with areas and energy and defines the spatial parameters of the moving vehicles and their travel domain. Uncertainty is overcome by proper dissemination of information about departure gates and times. For informational purposes it is best to have a high concentration of people in the center of the terminal. Everyone must find where his/her departure gate is located in the terminal, or, when deplaning, where to pick up the luggage and locate a limousine or other surface transportation contact. The terminal is the space where this sorting occurs. Unfortunately the cost of addressing the first two types of travel efforts: acceleration and uncertainty are substitutable by the third cost of queuing. Capacity of structures, number of runways, departure gates, luggage carousels, storage, announcements, open ticket counters can all be smaller, fewer, and have less capacity by making the passengers, surface vehicles and aircraft wait in lines. Because the aircraft and surface vehicles have such different passenger capacities, and because of favored times of day for departures, holding areas, waiting rooms and long lines are an inevitable part of the travel effort to move from one travel domain to another.
Spatial Analysis and Spatial Design
The terminal building is the permeable membrane or interface that facilitates the exchange between surface vehicles and aircraft. Do airport have to be kidney-shaped? Certainly not, but it helps if they are because the shape is an optimum pattern for accommodating flows near and through the boundary of two media with different spatial parameters. Understanding spatial systems through such analysis informs one about possibilities for spatial design. When teaching GIS courses I find that applying spatial analysis to design problems carries one beyond technique and often provides a sense of surprise and satisfaction. I delight in finding connections between unlike things where the connections are the consequence of abstract spatial p roperties.
References.
Arlinghaus, Sandra L. and John D. Nystuen "Geometry of Boundary Exchanges," The Geographical Review v. 80 no. I (January 1990), pp. 21-31.
Mercer, Paul F. and R. H, Wasserman, "Autoradiographic Distribution of Radioactive Sodium in Rat Kidney," Science vol. 143 (14 Febmary 1964): 695-696.
Nystuen, John D., "Boundary Shapes and Boundary Problems," Peace Research Society International, v. 7 (1967): 107-128.