Use the back button on your browser to return to this review.
http://wildegg.com
http://web.maths.unsw.edu.au/~norman/
email: n.wildberger@unsw.edu.au

The new form
of trigonometry developed here is called rational trigonometry, to
distinguish it from classical
trigonometry,
the latter involving cos 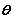 , sin
, sin 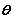 and the many trigonometric
relations
currently taught to students. An essential point of rational
trigonometry is that quadrance and spread, not distance and angle, are
the right concepts for metrical geometry (i.e. a geometry in which
measurement is involved).
and the many trigonometric
relations
currently taught to students. An essential point of rational
trigonometry is that quadrance and spread, not distance and angle, are
the right concepts for metrical geometry (i.e. a geometry in which
measurement is involved).
Quadrance and spread are quadratic quantitites, while distance and angle are almost, but not quite, linear ones. The quadratic view is more general and powerful. At some level, this is known by many mathematicians. When this insight is put firmly into practice, as it is here, a new foundation for mathematics and mathematics education arises which simplifies Euclidean and non-Euclidean geometries, changes our understanding of algebraic geometry, and often simplifies difficult practical problems. Quadrance measures the separation of points, and spread measures the separation of lines.
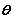 , sin
, sin 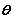 and the many trigonometric
relations
currently taught to students. An essential point of rational
trigonometry is that quadrance and spread, not distance and angle, are
the right concepts for metrical geometry (i.e. a geometry in which
measurement is involved).
and the many trigonometric
relations
currently taught to students. An essential point of rational
trigonometry is that quadrance and spread, not distance and angle, are
the right concepts for metrical geometry (i.e. a geometry in which
measurement is involved).Quadrance and spread are quadratic quantitites, while distance and angle are almost, but not quite, linear ones. The quadratic view is more general and powerful. At some level, this is known by many mathematicians. When this insight is put firmly into practice, as it is here, a new foundation for mathematics and mathematics education arises which simplifies Euclidean and non-Euclidean geometries, changes our understanding of algebraic geometry, and often simplifies difficult practical problems. Quadrance measures the separation of points, and spread measures the separation of lines.
What makes sense for the student and researcher from an intuitive standpoint may not, however, make sense to those who are set within rigid institutional guidelines in academic curricular development or in academic publishing. Imagine a world in which conventional trigonometry and its representation is no longer the norm. All books that use these functions must now be rewritten--perhaps a fine opportunity for the world of electronic publishing in which mathematics can come to life through animation, virtual reality, and other state-of-the-art tools.
While this latter prospect of extensive document conversion is a daunting one, that would seem unlikely to happen based on the presence of a single work adopting the "quadrature" and "spread" approach, those in disciplines such as mathematical geography that have relatively little invested in traditional institutional rigidity have an opportunity to integrate promising new conceptual approaches into our own theoretical work. If we demonstrate great success, then others more steeped in convention, may see merit in the approach for their own research.
The implications for mapping, of the earth-sphere to the plane, might be probed: what would a "sinusoidal" map look like when expressed in terms of "spread"? One would expect the same map would result using either approach but the route by which one gets there would be different. The history of our discipline is one that is rich in example of the merit of exploration, field study, and different paths: these terms need not be confined to the "real" world but apply equally in the world of the mind.
For example, looking at existing maps within a different light might open up deep and interesting cartographic research areas. Further, one might imagine a total recasting of the graticule in which rotation matrices contain no trigonometric functions so that even a beginning student can flip from one earth-based coordinate system to another in a somewhat intuitive manner. As we, on planet Earth, continue to look outside toward other planets, theoretical material that makes modeling more intuitive is important--indeed, it is critical.
Sandra Lach Arlinghaus
Ann Arbor, MI