A scatter of dots might represent any real world phenomenon:  from the location of emergency telephone kiosks, to small villages, to national capitals.  Dots pinpoint geographic position.  At a global scale, national capitals may appear as dots; at a local scale, they may appear as areas containing dot scatter of their own.  What matters is geographic scale:  dots at one scale may not be dots at another scale.  In that regard, it does not matter what the dots represent.

Dot density maps
Dot density maps might show 1 dot representing 200 people in some spatial unit or 1 dot representing 1 percent of the population of yet another spatial unit. One might see a map in a newspaper showing concentrations of voters of different political persuasion, by ward, prior to an election.  Often, though, these maps might appear to be (or actually be) in error:  a glance at one's own home ward generally elicits reactions such as "no one lives over there where that dot is!"  Dot density maps should not be confused with pushing pins in a wall map to indicate position; dot density maps show pattern, not specific position tied to address or latitude/longitude. When the dot density map is properly constructed it can serve as a tool offering valuable insight into clustering.  A variety of examples are shown below: they range in scale from a local neighborhood example, centered on Hyde Park (in Chicago, Illinois, USA) the University of Chicago neighborhood,  to the city level, to the state level, to the watershed level.  The lessons they suggest should lure the thoughtful reader away from error in interpretation and use.

Nested Hierarchies of Polygons
To be effective, the dot scatter should be randomized at a relatively local scale and then viewed for pattern at a scale more global than the scale of randomization. In Figure 1, dot scatter has been randomized at the U.S. Census Block Group level; it is then viewed successively at the U.S. Census Tract level (tracts are larger than block groups) and then at the state level (in the animation):  a hierarchy of regions. Any pattern in the scatter of dots within individual block groups is meaningless: the scatter is random. Within tracts, broad clusters, or centers of activity, are evident; and, even more obviously within the state, clusters of dots delineate urban (central) areas.

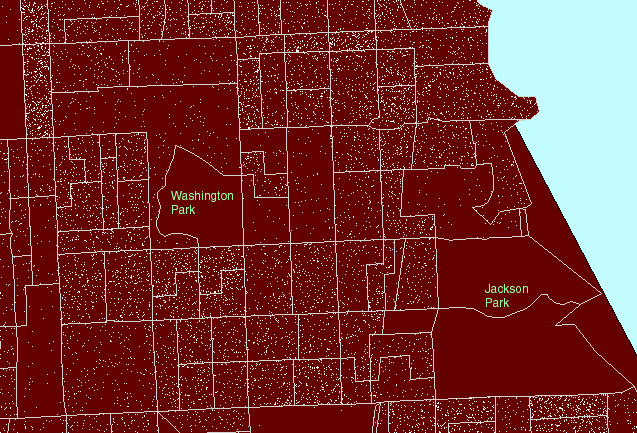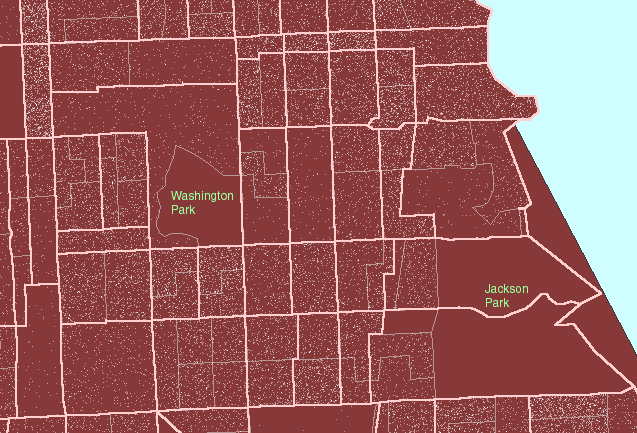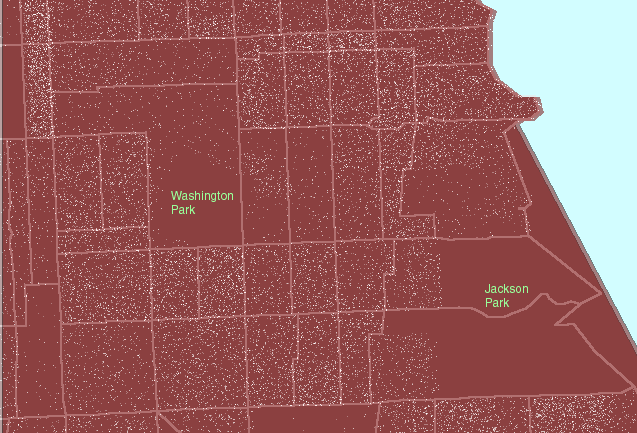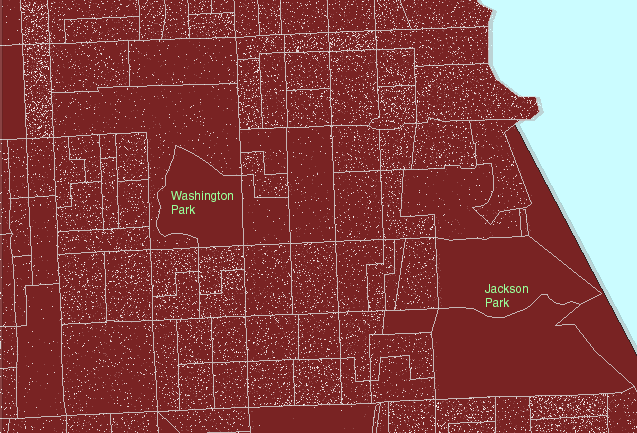
Figure 1.  A local view:  Hyde Park lies roughly between Jackson Park on the east and Washington Park on the west.  US Census block groups are shown in gray outline. US Census tracts are shown in heavier pink outline. (First frame in the animated map shows dot scatter in block groups.)

For the clustering of dot scatter to have meaning, look at it, for example, through the lens of the more regional US Census tract boundaries (heavy pink lines in Figure 1).  Figure 1 moves the reader's eye from block group boundaries, to block group boundaries nested inside tract boundaries, to tract boundaries alone, to no boundaries.  As boundaries increase in generality, and dot scatter remains the same, clustering of dots becomes sensible.  Thus, in Figure 1, one sees no dots in the block groups containing Jackson Park and Washington Park so that when the block group boundaries are replaced by tract boundaries, which contain the park and dwelling units, the dots are not scattered across the park but remain in the region of the tract where people live.  The clustering to the west of Jackson Park means something at the tract level.

The pattern of boundary removal, to make sense of dot scatter, is not symmetric.  In Figure 1, dots were randomized at the block group level and then viewed at the tract level.  Because

• tracts are larger than block groups, and
• block groups are nested within tracts

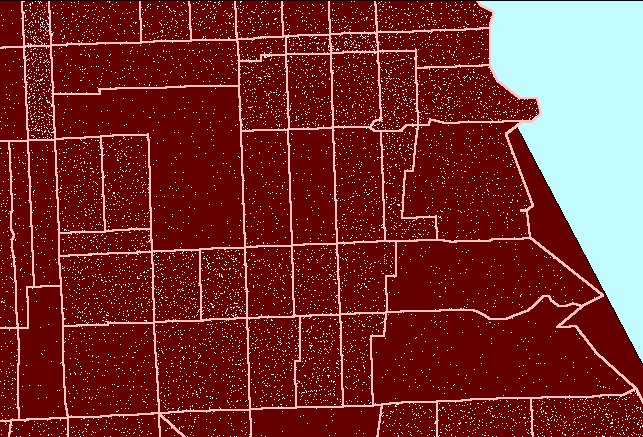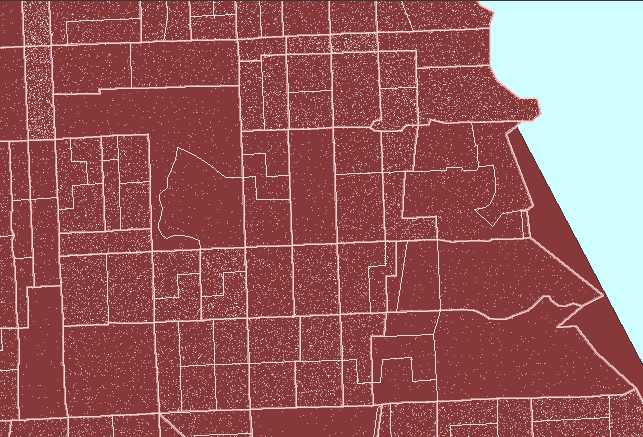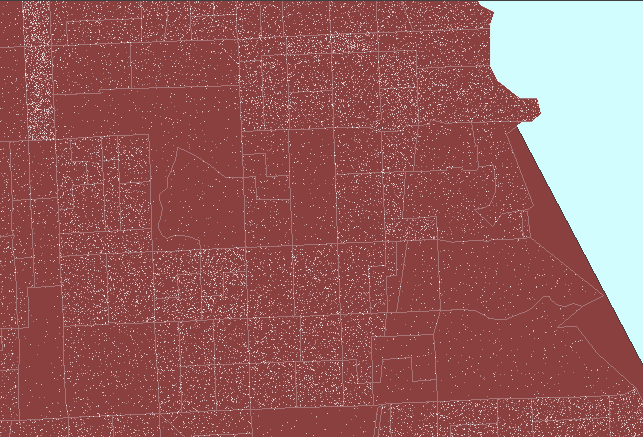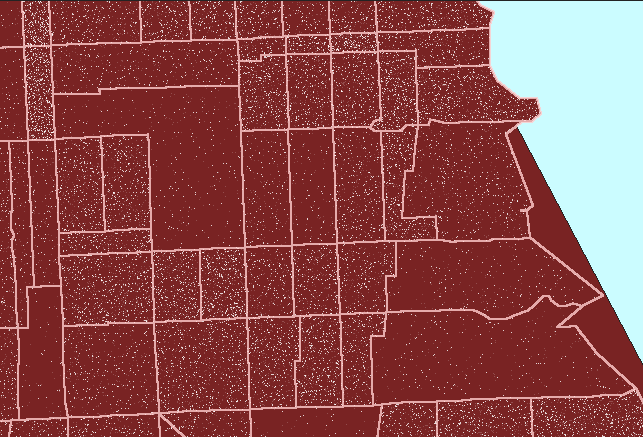
Figure 2.  Dot scatter is randomized at the tract level and then viewed within block group boundaries causing error in assigning dwelling units (people) to parkland.  (First frame in the animation shows dot scatter in tracts outlined in pink.)

Principle 1: Randomizing Principle
In a dot density map, dot scatter is randomized at one scale and then, to have the map make sense, must be viewed at a scale more global than that of the randomizing layer.

A dot density map that is constructed to follow Principle 1 will be said to be a "properly constructed" dot density map.  Any that does not follow Principle 1 will be viewed, therefore, to be improper and likely to convey error.

In a properly constructed dot density map, if a more global layer is composed of polygons that contain the randomizing layer in a nested fashion, then there is no problem of overlapping regions and possible confusion about assignment of dot to polygon.  Thus,

Principle 2: Optimization Principle
A nested hierarchy of layers provides optimized assignment of dots to more global layers.

A dot density map that is constructed to follow Principle 1 and Principle 2 will be said to be an "optimized properly constructed" dot density map.  In the next section, example will be given of a properly constructed dot density map that is not optimized.

Hierarchies with Overlapping Layers
Often, unfortunately, one is not able to obtain data arranged in a nested spatial hierarchy, such as the tract and block group units shown above.  It may be desired, for example to use Census data to obtain information about zip code polygons, school districts, minor civil divisions, and so forth.  Census boundaries, however, are not generally commensurate with zip code boundaries and various other spatial units.

There are a number of ways of extracting information from Census units about, for example, zip code areas.  One way involves using computer software to calculate the centroids of Census units and count the Census unit as lying "within" the zip code area if the centroid of the Census unit lies within the zip code area.  Zip code areas are often larger than tracts and block groups, especially in urban areas (as Census units are scaled in area according to population).  Thus, in an urban setting, one might properly construct a dot density map randomizing the dot scatter at the block group level and then viewing that scatter through tract boundaries and ZIP code boundaries, creating a properly constructed dot density map that is not optimized because the hierarchy of spatial units on which it is based is not a nested hierarchy.   Figure 3 illustrates the process for a region on the south side of Chicago centered on Hyde Park.

 

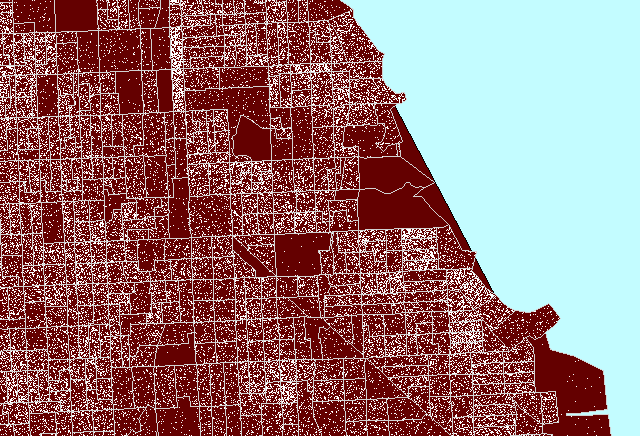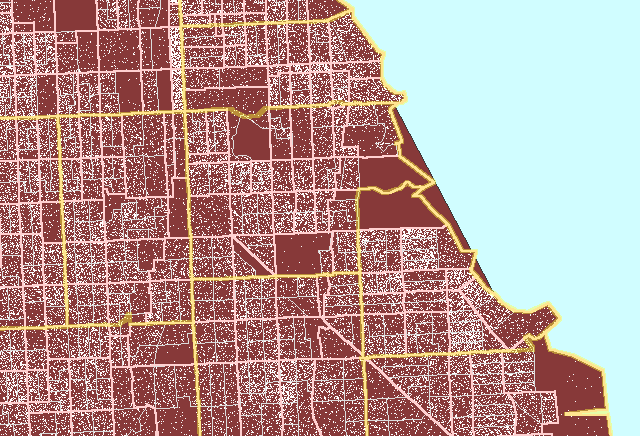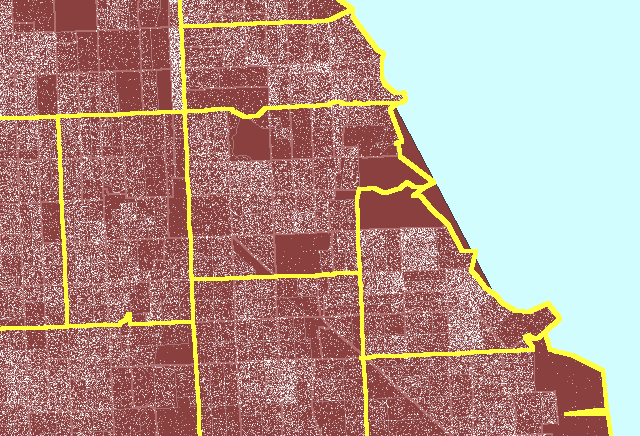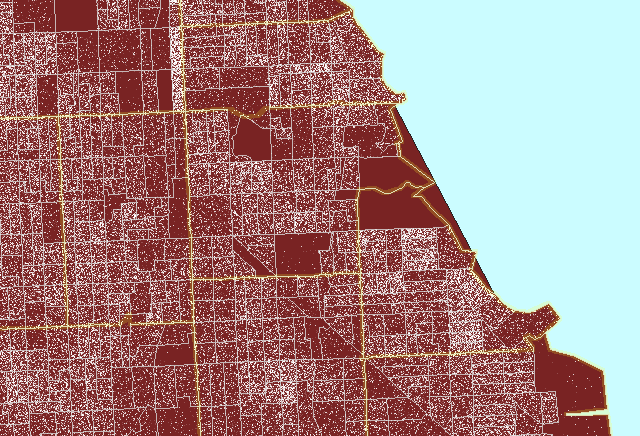
Figure 3.  Zip code boundaries (yellow) do not match either Census tract (pink) or Census block group (gray) boundaries.  (First frame in the animation shows dot scatter in block groups.)   An example of a properly constructed dot density map that is not optimized.

Scale Change
Beyond the two principles above, there are a number of other issues to consider when using a properly constructed dot density map.  Often, randomizing at the most local level is best.  When one looks at a more regional view, however, local randomization may introduce clutter into the map.  In Figure 4 the scale has been made more global to include much of the Chicago metropolitan area.  In that view, the white dots nearly fill space and clustering is not evident.  Conceptually, in order to reduce dot clutter, one might randomize at a more global level or one might alter what the dots represent.  Sacrifice in accuracy of dot position always undermines the fidelity of the dot density map; alter what the dot represents, instead of its position.

Principle 3:  Scale Principle
When a change in scale produces dot clutter from dot density, randomize at the most local scale available and alter dot representation to retain a properly constructed dot density map.

 

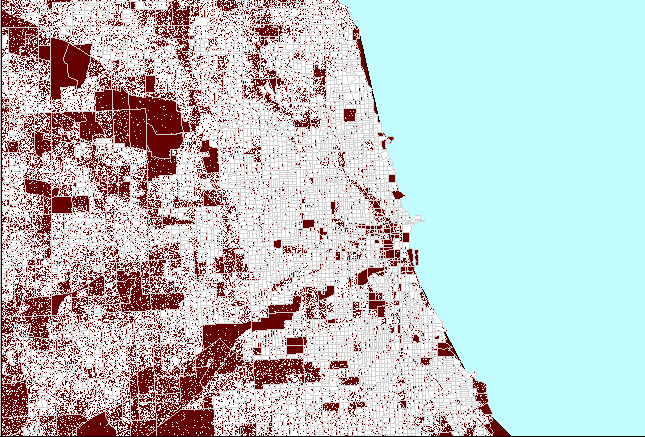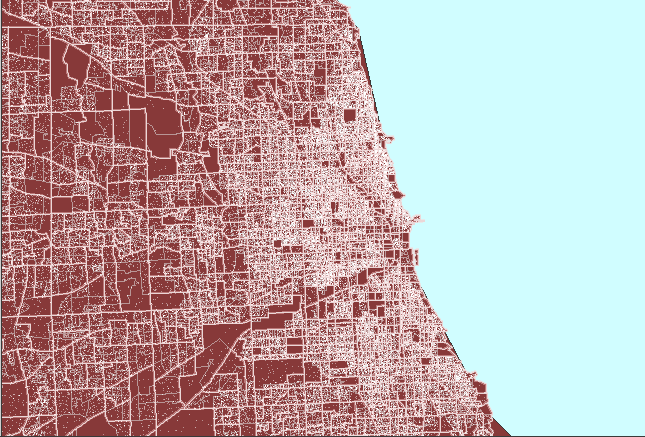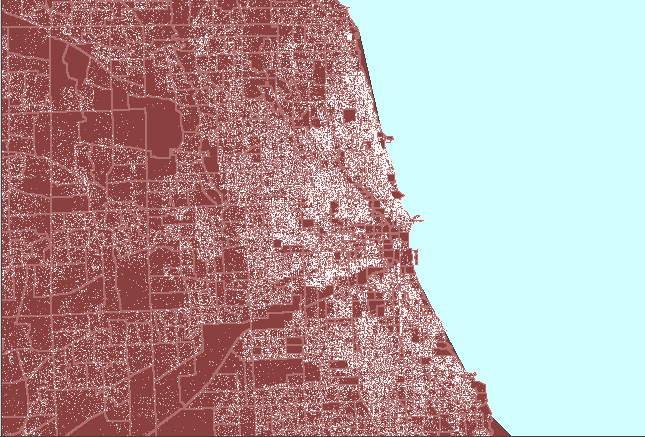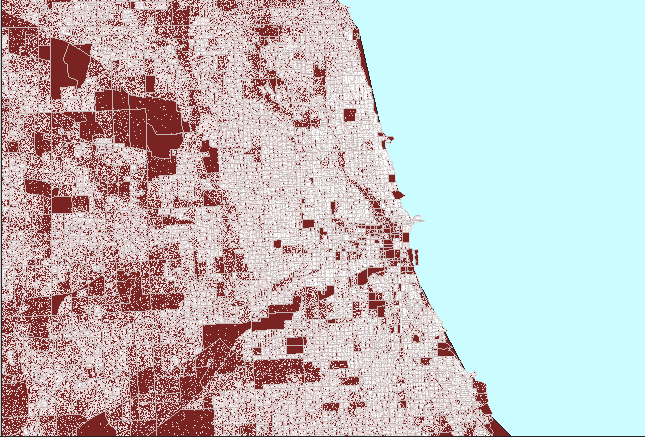
Figure 4.  Dot clutter followed by a properly constructed dot density map of Chicago, Illinois.  (First frame in the animation shows heavy white dot scatter in block groups.)

The animated map in Figure 4 shows dot clutter resulting from using 1 dot to represent 10 people.  A better choice, at this scale, of 1 dot to represent 100 people reduces the number of dots by a factor of 10 so that clusters become evident, particularly when no Census boundaries are overlain.  In both cases, the dot scatter is randomized at the block group level: the most local level for which data was readily available in this example.  Thus, there is no sacrifice in accuracy of dot position in removing dot clutter by thinning the number, rather than by altering the position, of dots.

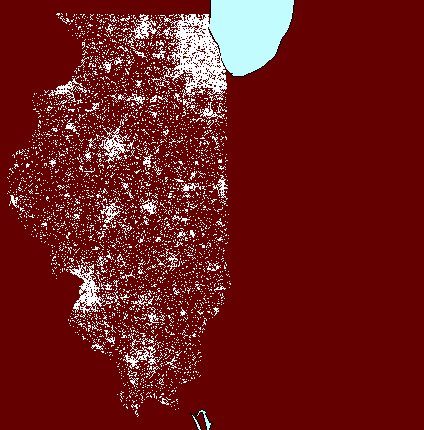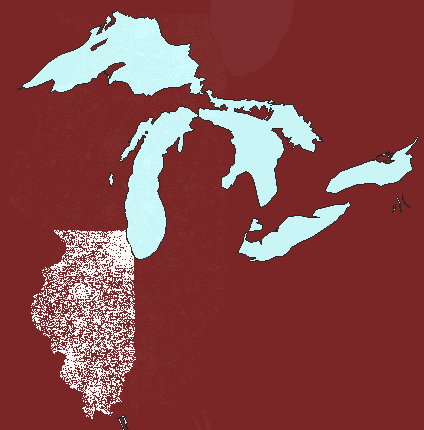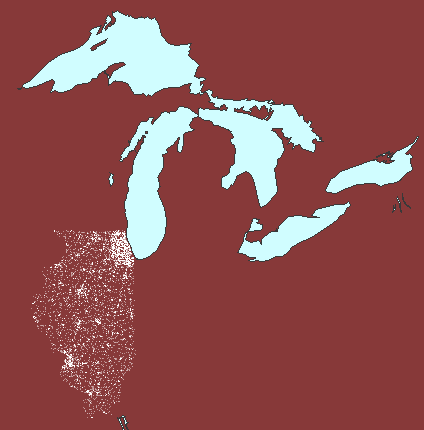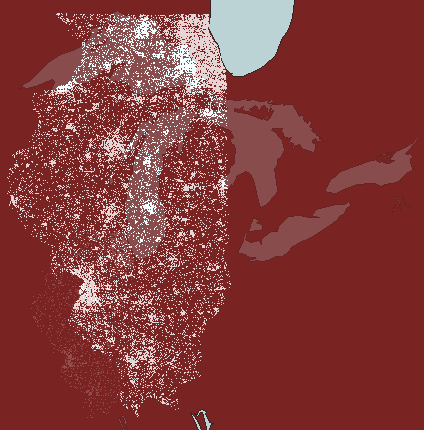
When the '1 dot to represent 100 people' representation is transformed to the state level, portrayal of urban areas is evident.  Dot clutter, from this particular representation, once again enters the picture at the watershed level (Figure 5).  The first watershed frame in Figure 5 shows Illinois at 1 dot to 100 people: dot clutter obscures dot clusters.  The second watershed frame shows Illinois at 1 dot representing 1000 people: dot thinning may appear to have removed clusters.  The final frame shows a compromise at 1 dot representing 800 people:  a view that reduces dot clutter yet retains dot clusters.

 

Figure 5.  Change in scale and dot scatter thinning.  (First frame in the animation shows only the state of Illinois.)

The Importance of the Equal Area Projection
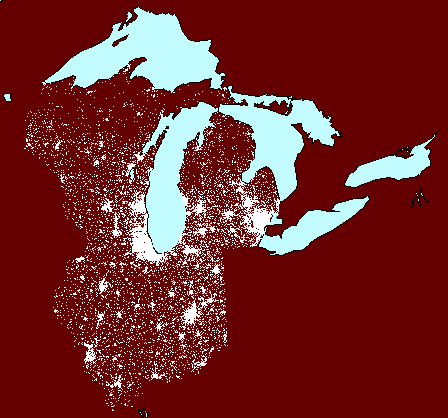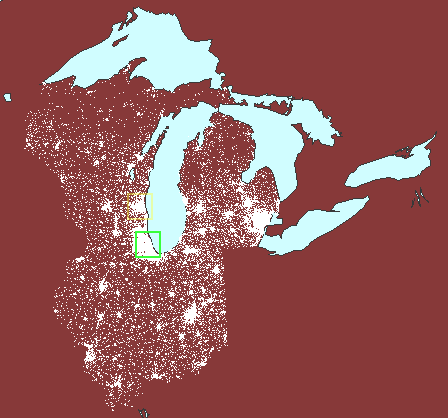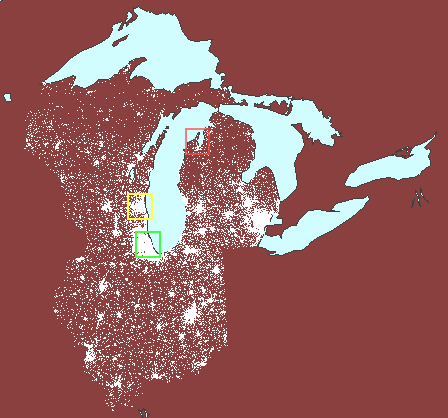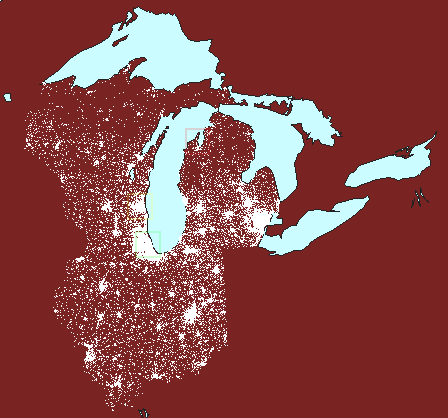
Map projections on which a geometric unit square represents the same amount of geographic area, independent of position, are called "equal area projections."  On an equal area projection, relative land mass sizes appear as they do on the globe:  Brazil is larger than Greenland, for example.  Dot density maps can be used to make comparisons; the animated map below (Figure 6) suggests comparing population (either as total numbers or as a percentage) in Chicago (green square) to that of Milwaukee (yellow square) and Traverse City (red square).  The underlying projection employed is an Albers equal area projection.  Thus, the squares represent the same amount of area on the earth and comparisons at different latitudes are valid. Had a Mercator projection (for example) been employed, the red square would have represented less geographic area than would have the green square and comparisons based on area would have been invalid.

 

Figure 6.  Valid comparisons of dot scatter using an equal area projection:  Chicago (green), Milwaukee (yellow), and Traverse City (red).  (First frame in the animation shows dot scatter surrounding Lake Michigan with no extra polygons.)

Principle 4:  Projection principle
A properly projected dot density map must be based on an equal area projection.

If any projection other than an equal area projection is employed in making a dot density map, then comparisons involving area will be in error.

In order of importance the Principles for making these maps are:

• If dot density maps are to be properly constructed, then they must follow Principle 1:  Randomizing Principle
• If dot density maps are to be used to make comparisons involving area, then they must follow Principle 4:  Projection Principle
• If dot density maps are to optimize assignment of dot pattern, then they must follow Principle 2:  Optimization Principle
• If dot density maps are to succeed in transcending scale change, then they must follow Principle 3:  Scale Principle

Interactive Maps
Interactive maps are tools that may offer both vertical and lateral movement within a hierarchy.  Figure 7 shows a screen shot of an interactive map that includes state boundaries (heavy white lines), county boundaries (yellow lines), Census tract boundaries (pink lines), and dot scatter at the 1:800 level as in Figure 5 above.  Click on this link to go to the map in its interactive form.  Once there,  use the zoom feature to shift hierarchical levels in a scale transformation.  Within a given hierarchical level, click on single polygons to view associated database information.  Or, search the underlying database using the "search" feature to find polygons with attributes of special interest.   In this instance, the technological realm offers a form of spatial synthesis not available in the classical realm.
 

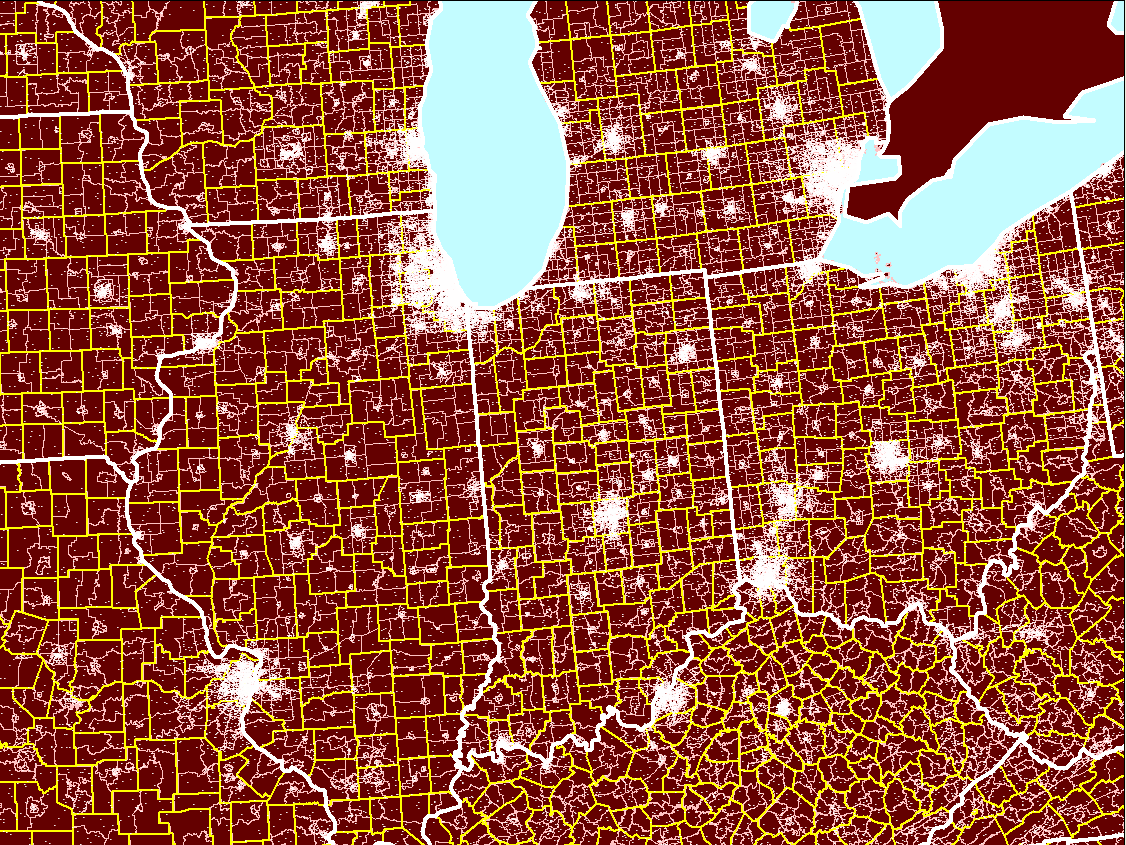
Figure 7. An example of a dot density map that follows all four basic principles.  State boundaries in white contain county boundaries in yellow which in turn contain tract boundaries in pink.  Click on the map to go to the associated interactive map.

---

Sarastro:  Die Strahlen der Sonne vertreiben die Nacht
Background music that launches when the title is clicked is a sample from advertising on Amazon.com from the following link:
http://www.amazon.co.uk/exec/obidos/ASIN/B000001GXI/qid=1115239267/sr=8-2/ref=sr_8_xs_ap_i2_xgl/026-8133798-8086815

(Die) Zauberflöte, '(The) Magic Flute'

798-8086815
Die Zauberflöte (The Magic Flute), opera, K. 620
Composer: Wolfgang Amadeus Mozart
Conductor: Karl Böhm
Performers: Evelyn Lear, Roberta Peters, Lisa Otto, Fritz Wunderlich, Dietrich Fischer-Dieskau, Franz Crass, Hans Hotter, Friedrich Lenz, Hildegard Hillebrecht, Cvetka Ahlin, Sieglinde Wagner, Rosl Schwaiger, Antonia Fahberg, Raili Kostia, James King, Martti Talvela, Hubert Hilten, Martin Vantin, Manfred Röhrl
Orchestra: Berlin Radio Chamber Choir, Berlin Philharmonic Orchestra
Label: The Originals
Catalogue Number: 4497492 
Released: February 10, 1997 
Audio CD A-D 
Number of Discs:2 
ASIN: B000001GXI