Hexagonal Hierarchies and Close Packing of the Plane:  Overview
      A scatter of points, spread evenly across the plane, may take on a variety of configurations:  two simple regular lattices involve points that suggest squares or equilateral triangles.  If one wishes to consider circular buffers around each point, then these buffers may overlap or be widely spaced.   A natural issue to consider is to provide some sort of maximal coverage of the plane by the buffers:  to provide a "close packing" of the plane by circles. Gauss (1831/40) proved that the densest lattice packing of the plane is the one based on the triangular lattice.  In 1968 (and earlier), Fejes-Toth proved that that same packing is not only the densest lattice packing of the plane but is also the densest of all possible plane packings.  If one thinks, then, of the circles as if they were bubble foam, the circles centered on a square grid pattern expand and collide to form a grid of squares (Boys).  The circles centered on a triangular grid pattern expand and collide to form a mesh of regular hexagons, like the cells in a slice of the honeycomb of bees (de Vries).  The theoretical issues surrounding tiling in the plane are complex; even deeper are those issues involving packings in three dimensional space.  The reader interested in probing this topic further is referred to the Bibliography at the end of this document.  Interpretation of the simple triangular grid has range sufficient to fill this document and far more.

Classical Urban Hexagonal Hierarchies
     One classical interpretation of what dots on a lattice might represent is found in the geometry of "central place theory" (Christaller, Lösch).  This idea takes the complex human process of urbanization and attempts to look at it in an abstract theoretical form in order to uncover any principles which might endure despite changes over time, situation, cultural tradition, and all the various human elements that are truly the hallmarks of urbanization.  Simplicity helps to reveal form:  models are not precise representations of reality.  They do, however, offer a way to look at some structural elements of complexity.  Thus, dots on a triangular lattice are populated places (often, villages).  Circles, expanding into hexagons, are areas that are tributary to the populated places.  In the traditional formulation (described after Kolars and Nystuen) one considers four basic postulates (no one of which is "real" but each of which is simple):

• The backdrop of land supports uniform population density
• There is a maximum distance that residents can easily penetrate into the tributary area.
• There is slow, steady population growth
• Village residents who move, as a result of growth (or for other reasons), attempt to remain in close contact with their previous location (to maintain social or other networks).

Suppose, in a triangular lattice of villages, that one village adds to its retailing activities.  After some time, growth occurs elsewhere.  How might other villages compete to serve tributary areas:  how will the larger, new villages share the tributary area?  The answers lead to a surprising number of possible scenarios.  Figure 1 shows the first in an infinite number of possibilities.  Animated locations, for competing larger villages, are shown in Figure 1.  The smallest villages are represented as small red dots; next nearest neighbors competing for intervening red dots are represented in blue; and, next nearest neighbors competing for intervening blue dots are represented in green.  Of course, one is usually only willing to travel so far to go to a place only slightly larger, so the fact that the animated pattern could be extended to an infinite number of levels, beyond green, may not mirror the second postulate.  Over time, however, one might suppose further growth and an entire hierarchy of populated places.
 

Figure 1.  A triangular lattice of dots with animated locations for competing locations entering and vanishing from the picture.

     Virtual reality is an exciting form of visualizing three dimensional objects.  Figure VR01 has a link on to a virtual reality view of that figure:  click on that figure to move into the virtual environment.  Imagine the dots are holes in a pasta machine through which the pasta dough is to be extruded as spaghetti:  the view in Figure 1 is the template and the linked virtual reality is the extruded pasta pulled through the red, blue, and green holes.   Drive through this landscape; think of the view as a skyline of cell towers or some other tall thin structures (Arlinghaus, 1993).  The placement of these towers is at vertices of equilateral triangles of various sizes forming an hexagonal hierarchy.
 

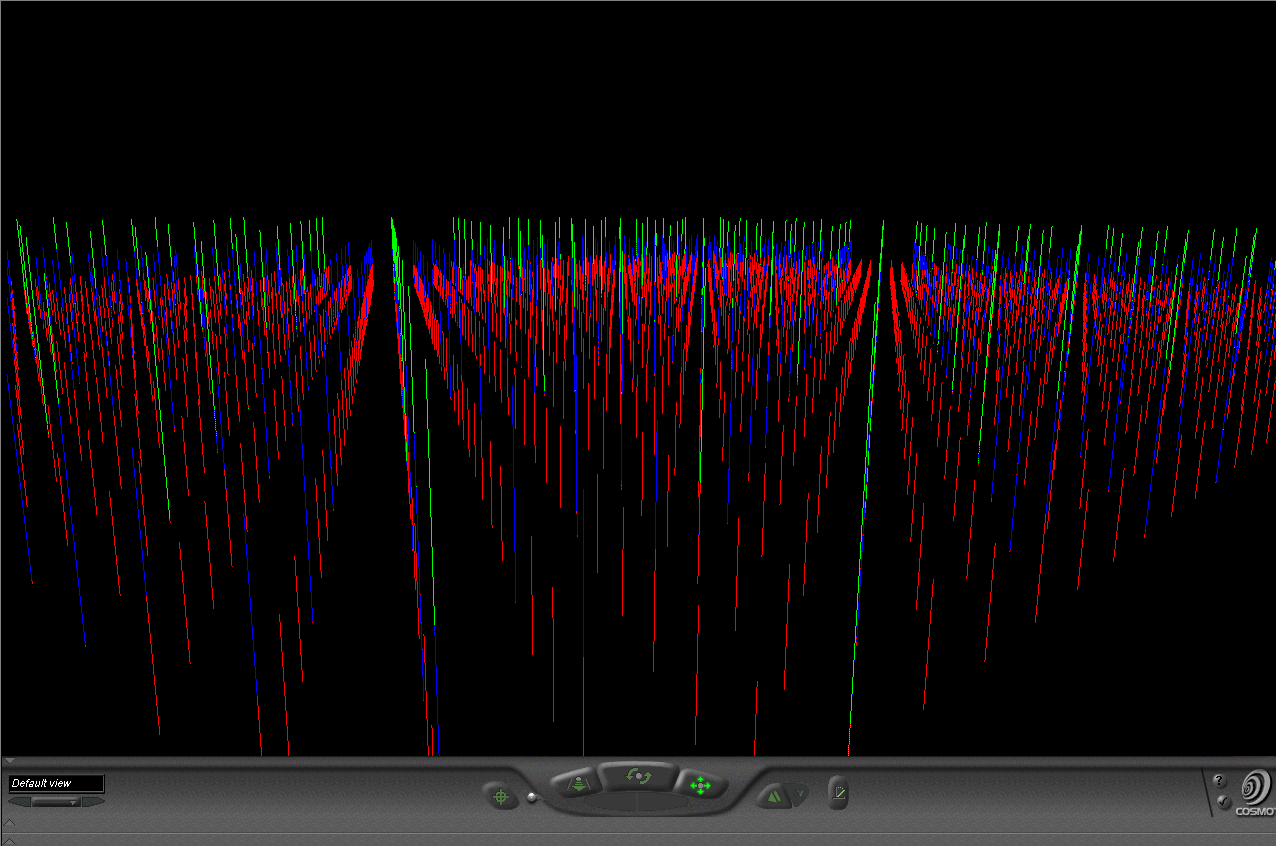Figure VR01.  A screen shot from the virtual world linked to this image.  Click on the image to enter that world!

     The pattern in Figure 1 suggests one arrangement for villages, towns, and cities.  We offer systematic visualization schemes for a variety of such arrangements:  first, following the classical approaches to this issue found in the works of Walter Christaller and August Lösch and, second, following the contemporary approach presented in previous conventional publications by the authors of this submission.

Visualization of Hexagonal Hierarchies using Animated Geometric Figures
Marketing principle:  K=3
     Consider a central place point, A, in a triangular lattice.  Unit hexagons (fundamental cells) surround each of the points in the lattice and represent the small tributary area of each village (Figure 2).  Growth at A has distinguished it from other villages in the system.  It will now serve a tributary area larger than will the unit hexagon. There are six villages directly adjacent to A.  The unit hexagons represent a partition of area based on even sharing of area between A and these six villages.  When A expands its central place activities, others may also desire to do so as well.  Figure 2 shows the locations for the next nearest competitors to enter the system.  Given that they, too, will share area evenly, a set of larger hexagons emerges.  Figure 3a shows the unit hexagons and the larger hexagons based on expansion of goods and services.   The competitors that enter are spaced at a distance, in terms of lattice points spaced one unit apart, of  units (Figure 2).  The position of the competitors that enter the system in this scenario are as close as possible to A; expansion of goods and services at any of the six closest neighbors would constitute no change in basic pattern.  One might imagine, therefore, that emphasis on distance minimization optimizes marketing capability--distance to market is at a minimum.
 
 

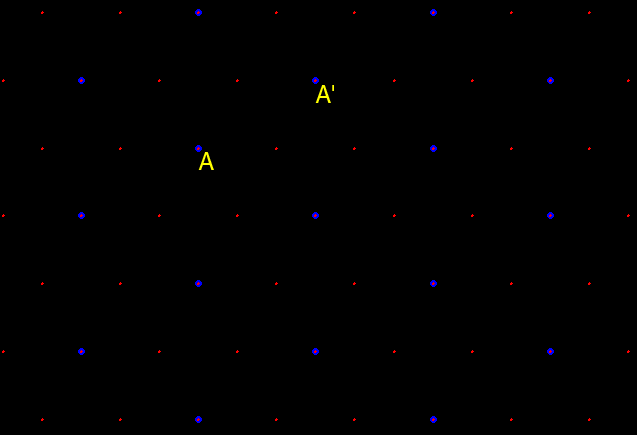Figure 2.  K=3:  Marketing.  Distance measurement between adjacent competing new centers, A and A':  in this case, competing centers, blue dots, are spaced  units apart, assuming a distance of one unit between adjacent red dots.

Thus, when competitors are chosen in this manner, the pattern of one layer of hexagons, in relation to another, has become known as a hierarchy arranged according to a "marketing principle" (Figure 3a).  Notationally, it is captured by the square of the distance between competing centers:  as a "K=3" hierarchy (Figure 2).  Each large hexagon contains the equivalent of three smaller hexagons.  One large hexagon = 1 small hexagon + six copies of 1/3 of a small hexagon = 3 small hexagons (Figure 3b, c, and d).  Thus, the value K=3 is not only related to distance between competing centers but also to size of tributary areas generated by competition:  as a constant of the hierarchy.

 

Figure 3a. K=3 hierarchy showing three layers of a nested hierarchy of hexagons of various sizes oriented with respect to one another according to the distance principle illustrated in Figure 2.

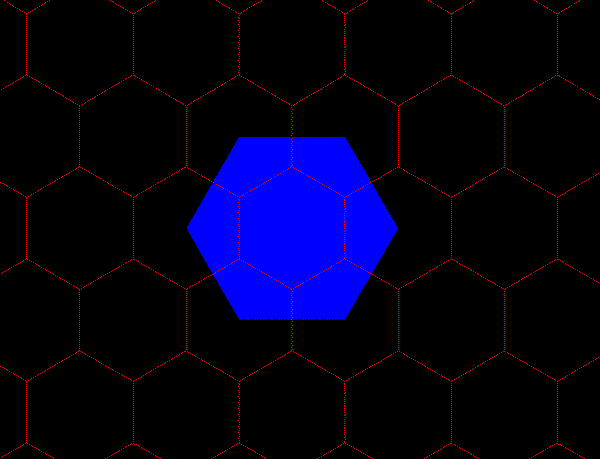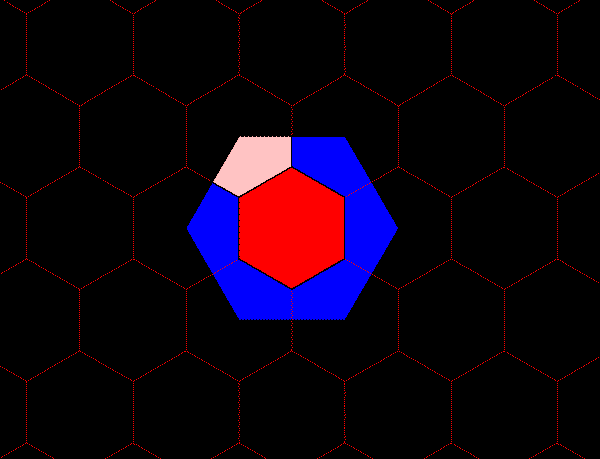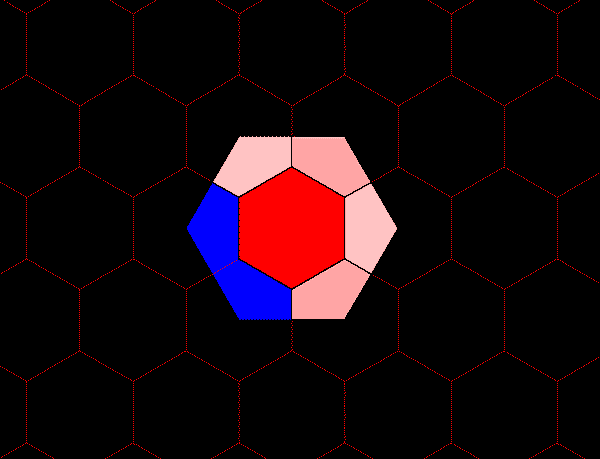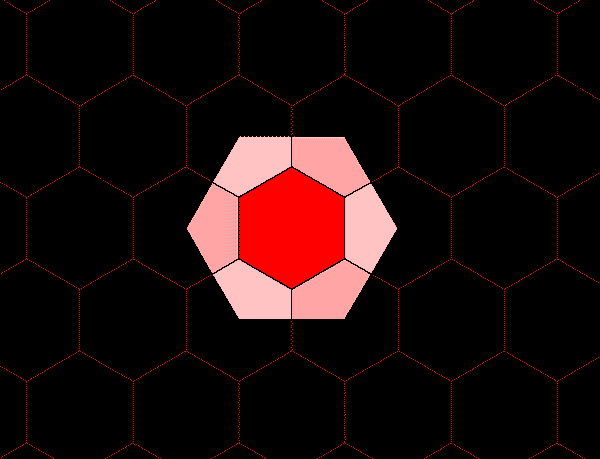Figure 3b.  Each blue hexagon contains the equivalent of three red hexagons:  one entire red hexagon surrounded by six copies of 1/3 of a red hexagon.

Figure 3c.  Each green hexagon contains the equivalent of three blue hexagons:  one entire blue hexagon surrounded by six copies of 1/3 of a blue hexagon.

Figure 3d.  The green hexagons contain the equivalent of 31 blue hexagons and 32 red hexagons.

Figure 4 shows the locations for the next nearest competitors, next beyond those from K=3, to enter the system.  Given that they, too, will share area evenly, a set of even larger hexagons emerges.  Figure 5a shows the unit hexagons and the larger hexagons based on expansion of goods and services.   The competitors that enter are spaced at a distance, in terms of lattice points spaced one unit apart, of 2 units (Figure 4).  The position of the competitors that enter the system in this scenario lie along radials that fan outward from A and pass along existing boundaries to tributary areas.  One might imagine, therefore, that emphasis on market penetration, or transportation, is the focus here.
 

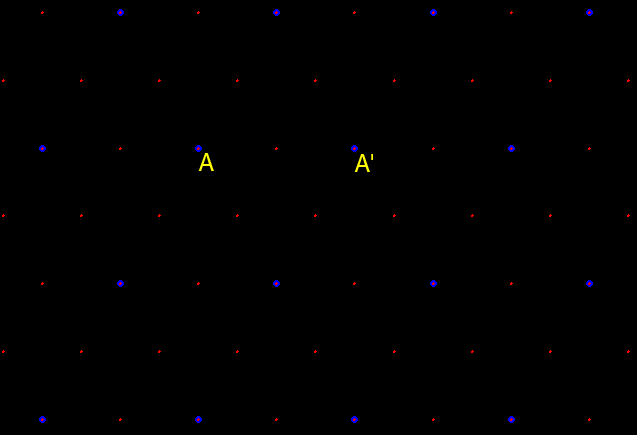Figure 4.  K=4:  Transportation.  Distance measurement between adjacent competing new centers, A and A' is 2 units, in this case (assuming a distance of 1 unit between adjacent red dots).

Thus, when competitors are chosen in this manner, the pattern of one layer of hexagons, in relation to another, has become known as a hierarchy arranged according to a "transportation principle" (Figure 5a).  Notationally, it is captured by the square of the distance between competing centers:  as a "K=4" hierarchy (Figure 4).  Each large hexagon contains the equivalent of four smaller hexagons.  One large hexagon = 1 small hexagon + six copies of 1/2 of a small hexagon = 4 small hexagons (Figure 5b, c, d).  Thus, the value K=4 is not only related to distance between competing centers but also to size of tributary areas generated by competition--as a constant of the hierarchy.

Figure 5a. K= 4 hierarchy showing three layers of a nested hierarchy of hexagons of various sizes oriented with respect to one another according to the distance principle illustrated in Figure 4.

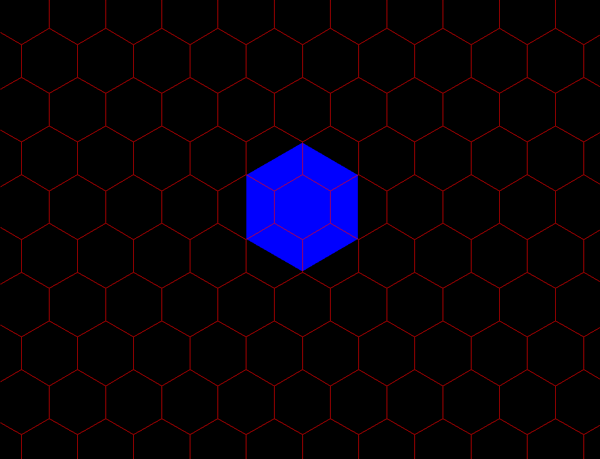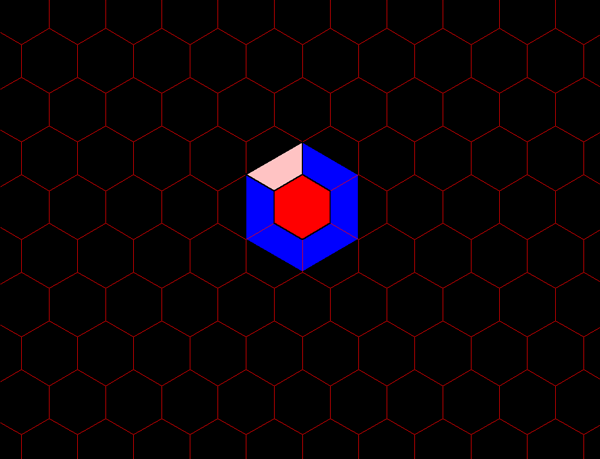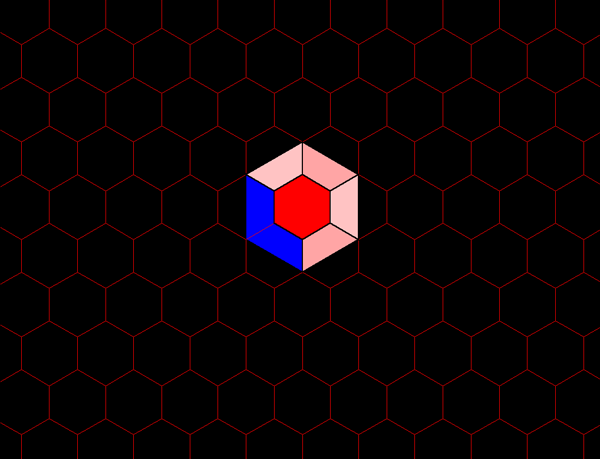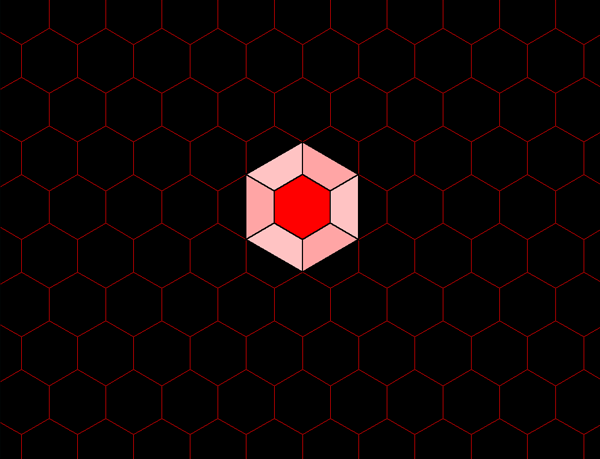Figure 5b.  Each blue hexagon contains the equivalent of four red hexagons:  one entire red hexagon surrounded by six copies of 1/2 of a red hexagon.

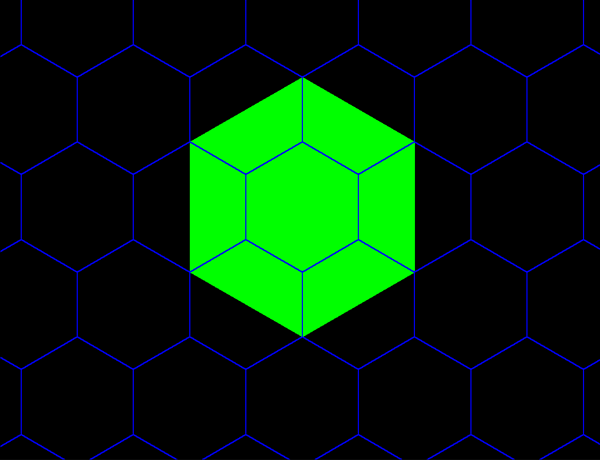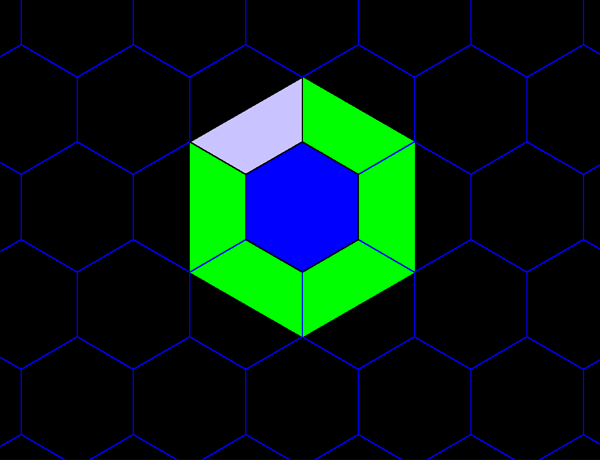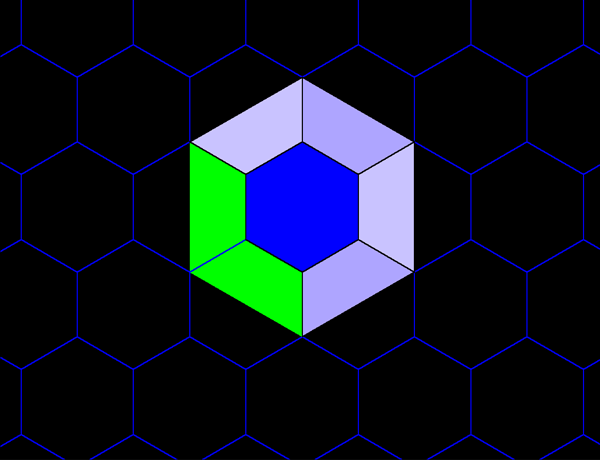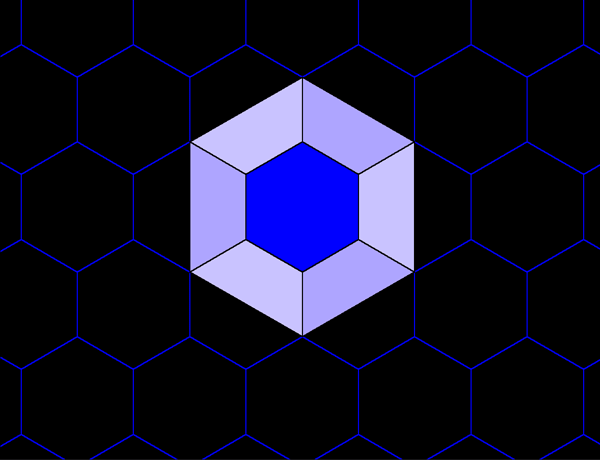Figure 5c.  Each green hexagon contains the equivalent of four blue hexagons:  one entire blue hexagon surrounded by six copies of 1/2 of a blue hexagon.

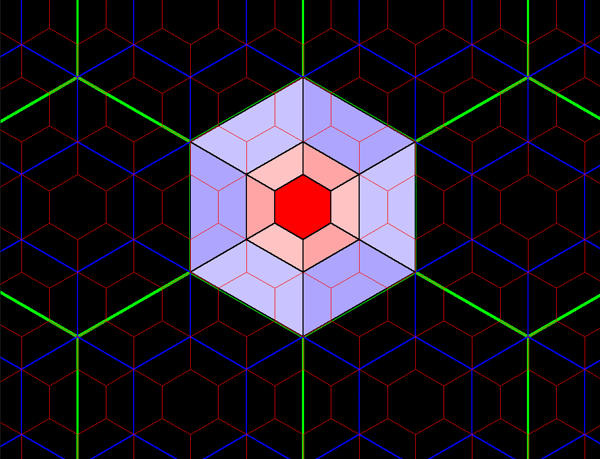Figure 5d.  The green hexagons contain the equivalent of 41 blue hexagons and 42 red hexagons.

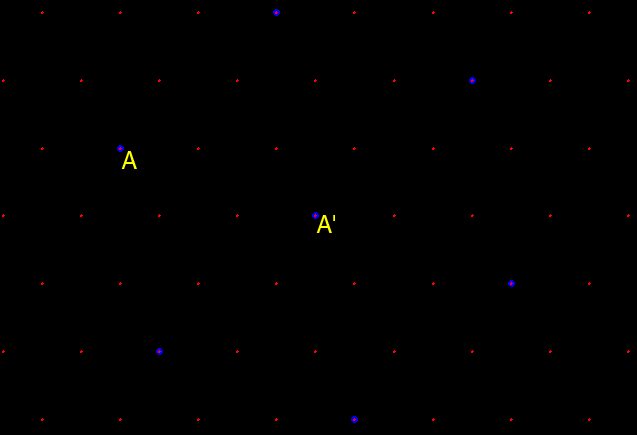Figure 6.  K=7:  Administrative.  Distance measurement between adjacent competing new centers, A and A' is  (assuming a distance of 1 unit between adjacent red dots).
 

Thus, when competitors are chosen in this manner, the pattern of one layer of hexagons, in relation to another, has become known as a hierarchy arranged according to an "administration principle" (Figure 7a).  Notationally, it is captured by the square of the distance between competing centers:  as a "K=7" hierarchy (Figure 6).  Each large hexagon contains the equivalent of seven smaller hexagons.  One large hexagon = 1 small hexagon + six copies of a small hexagon (underfit and overfit regions balance) = 7 small hexagons (Figure 7b, c, d).  Thus, the value K=7 is not only related to distance between competing centers but also to size of tributary areas generated by competition--as a constant of the hierarchy.

Figure 7a. K= 7 hierarchy showing three layers of a nested hierarchy of hexagons of various sizes oriented with respect to one another according to the distance principle illustrated in Figure 6.

Figure 7b.  Each blue hexagon contains the equivalent of seven red hexagons:  one entire red hexagon surrounded by six copies equivalent to a single red hexagon.  Each of the perimeter red hexagons is composed of 11/12 of a single red hexagonal cell plus 1/12 of an adjacent red cell:  in an underfit/overfit pattern.

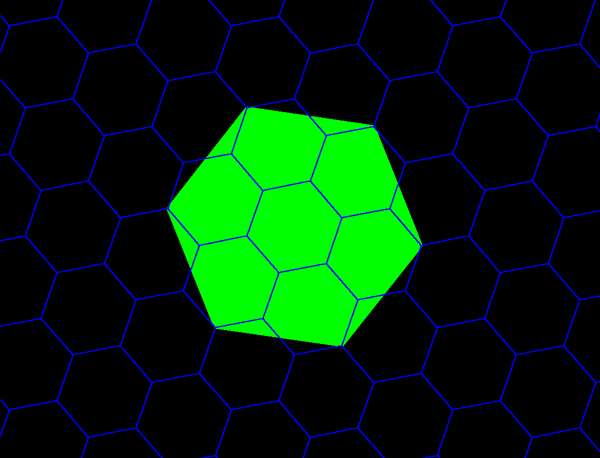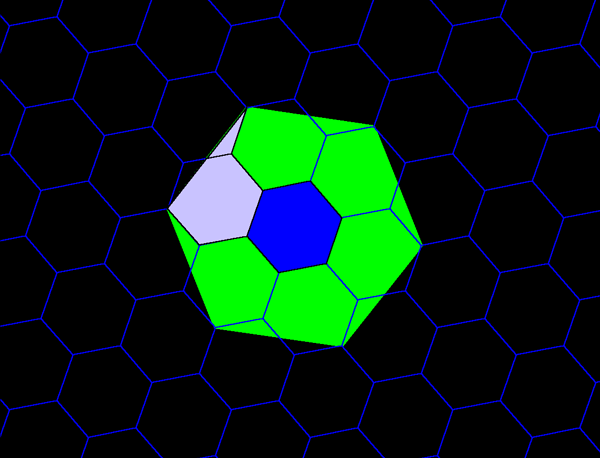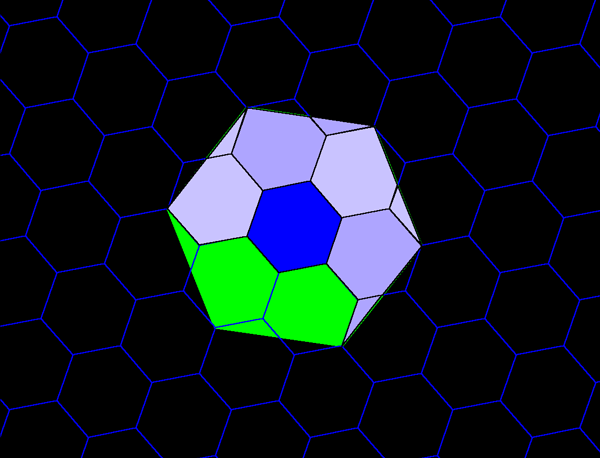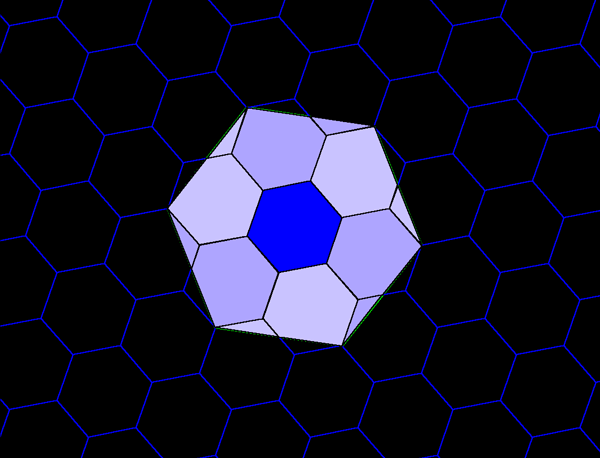Figure 7c.  Each green hexagon contains the equivalent of seven blue hexagons:  one entire blue hexagon surrounded by six copies equivalent to a single blue hexagon.  Each of the perimeter blue hexagons is composed of 11/12 of a single blue hexagonal cell plus 1/12 of an adjacent blue cell:  in an underfit/overfit pattern.

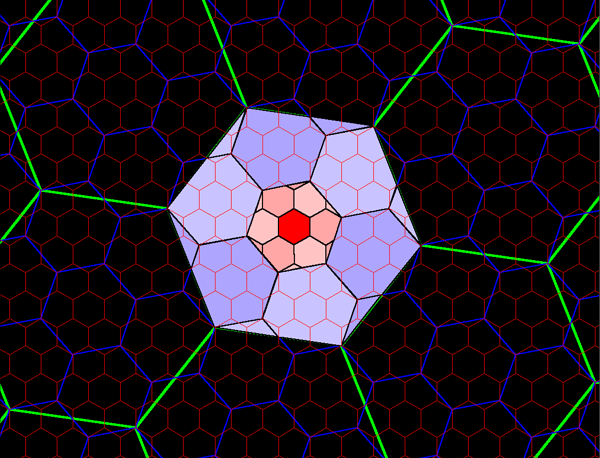Figure 7d.  The green hexagons contain the equivalent of 71 blue hexagons and 72 red hexagons.

• obtain as a base map a triangular lattice shape file; such a file may be created in ArcView using EdTools extension to precisely translate a point.
• ensure that each record in the underlying database has a unique code entered in "number" format (using the "add record number" feature of Animal Movement extension, if need be).
• if desired, create in a separate layer, a bounded region to serve as limits within which to calculate the landscape--a rectangle, for example.  One way to create such a region is to calculate the minimum convex polygon (convex hull) of the distribution of red dots using Home Range extension.
• load Spatial Analyst extension (ESRI) to ArcView and calculate Thiessen polygons using the Analysis|Assign Proximity command; choose the rectangle layer as the region within which to calculate the Thiessen polygons.  Alternately, employ the same strategy using Home Range extension and calculate Dirichlet regions.
• The result will appear as a set of small hexagons surrounding the dots, as in the red layers in Figures 2-7.
• Repeat the procedure on other triangular lattices, with broader spacing of lattice points as in the blue and green points above, derived from the base lattice.  The result will produce landscapes such as those in Figures 2-7 depending on how the broader spacing pattern is selected.

Visualization of Hexagonal Hierarchies using Mapplets
    Another method of visualizing hexagonal hierarchies, that is available only in current technology, looks simultaneously at connection patterns between multiple hierarchical layers of urban location maps and captures them as Java (TM) Applets:  as "Mapplets."  This process suggests a measure of visual stability of the geometric connectivity pattern that is related to the dimensions of the bounding box.  Figures 8, 9, and 10 show Mapplets for the K=3, K=4, and K=7 hierarchies, respectively.

 ...ONLY in the original...see caveat at top of page...

Figure 8.  K=3 Mapplet

Figure 9.  K=4 Mapplet

Figure 10.  K=7 Mapplet

Mapplets focus on connection patterns between successive hierarchical layers and, when K values are loaded as distances between hierarchies, they also suggest some elusive form of structural stability of geometric form.  Animated maps of the central place geometry of the plane, coupled with mapplets showing animated hierarchical pattern alone, suggest a three dimensional view of central place geometry.  A broader 3D view is suggested in the next section.

Visualization of Hexagonal Hierarchies using Animated Geometric Figures and Virtual Reality
     In the material below, we illustrate the use of the fractal concept of self-similarity to generate hexagonal hierarchies equivalent to those above, We use a hexagon as an initiator, and apply to it different selections of generators, to produce the different hexagonal hierarchies of classical central place theory (based on original concept and work of S. Arlinghaus).  In the previous sections we formed central place hexagonal hierarchies by moving from small hexagons to large ones; here, we reverse the process and dissect, using the self-similarity transformation, a large hexagon to create the smaller ones.  In both processes, the results correspond exactly.  The art is in generator selection, and it is simply that art that is presented in this chapter.  Later work delves into the mathematical foundations of that art.

The K=3 Hierarchy
     When an hexagonal initiator is chosen and a two-sided generator, with included angle of 120 degrees, is used to make successive replacement of the sides of the hexagon (as in the animated Figure 11a), the outline of the next layer of the K=3 central place hierarchy is generated (the black lines in Figure 11a suggest interior connections).  The replacement sequence applies the generator in an alternating pattern to the outside and then to the inside of the initiator.  When the original generator is scaled down, with shape preserved, and applied in the outside/inside sequence to the newly formed blue polygon, the next lower level central place K=3 hierarchy is formed (as in the animated Figure 11b).  The second, blue polygon contains three scaled-down hexagons, self-similar to the first hexagon (Figure 11a); the red polygon in the animation sequence contains three shapes self-similar to the blue polygon (Figure 11b), and 27 (or 3 cubed) hexagons self-similar to the original hexagon (Figure 11b).  The invariant of 3, in the K=3 hierarchy, is replicated in this particular fractal iteration sequence.

Figure 11a.  Animated K=3 fractal iteration sequence:  first transformation using a two-sided fractal generator applied successively to sides of the hexagonal initiator.

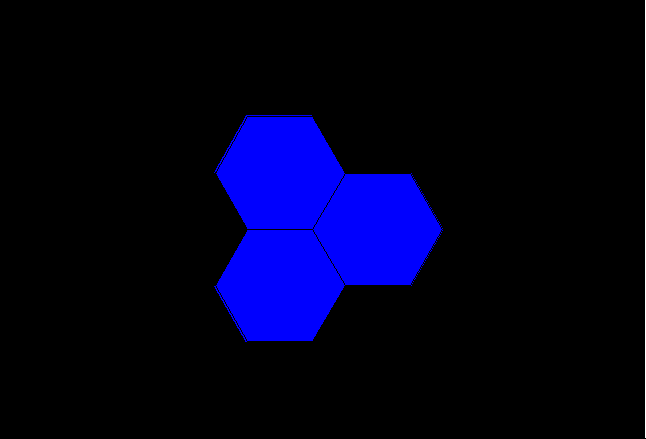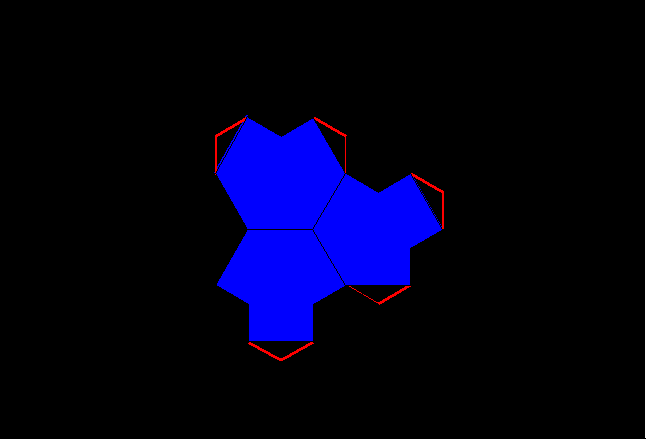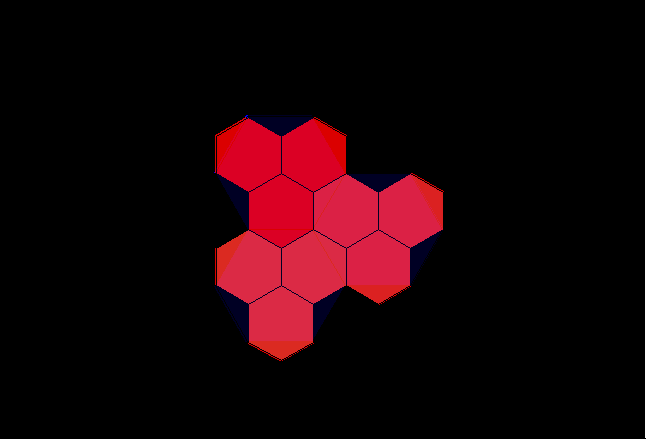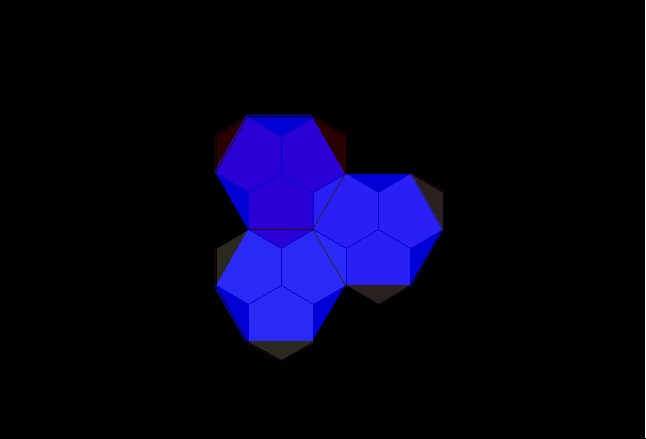Figure 11b.  Animated K=3 fractal iteration sequence:  second transformation using a scaled-down two-sided fractal generator applied successively to sides of the blue polygon generated in Figure 11a.

Figure VR02.  A screen shot from the virtual world linked to this image.  Click on the image to enter that world!

Figure VR03.  A screen shot from the virtual world linked to this image.  Click on the image to enter that world!  Translucent solids permit one to see relationships among layers of the hexagonal hierarchy while travelling through the solids.

Figure 12.  Fractally generated layers stacked on a single hexagonal tile.  Click here to see a virtual solid model of the tile with which the reader can interact. Click here to see a virtual translucent model of the tile with which the reader can interact.

Figure 13a.  Green layer on tile from Figure 12 fits exactly to tile the plane (Theorem of Gauss).

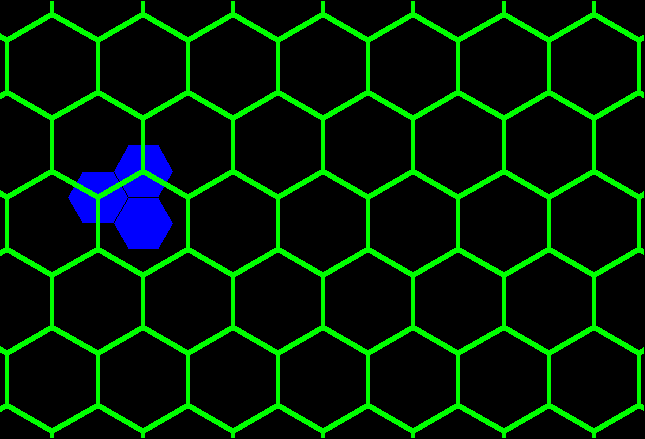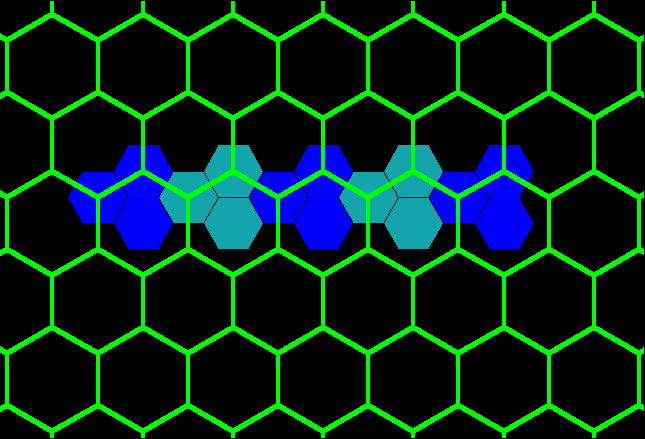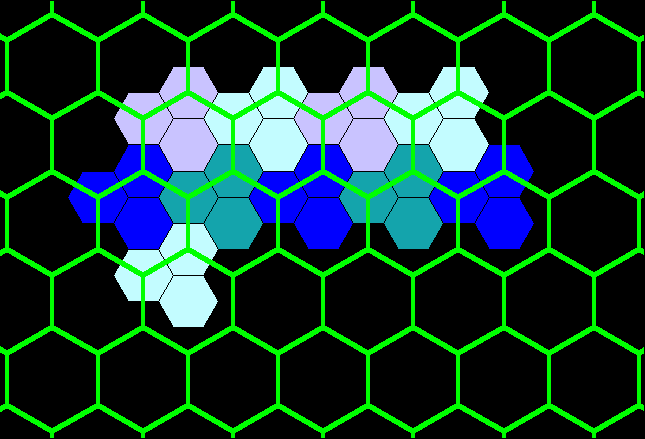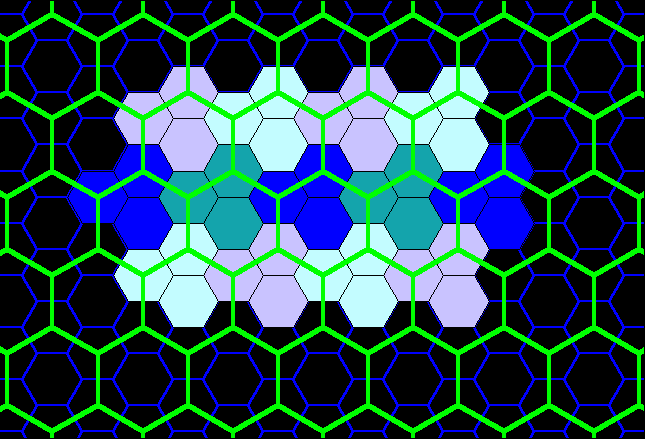Figure 13b.  Blue layer on tile from Figure 12 fits exactly to form classical K=3 landscape.

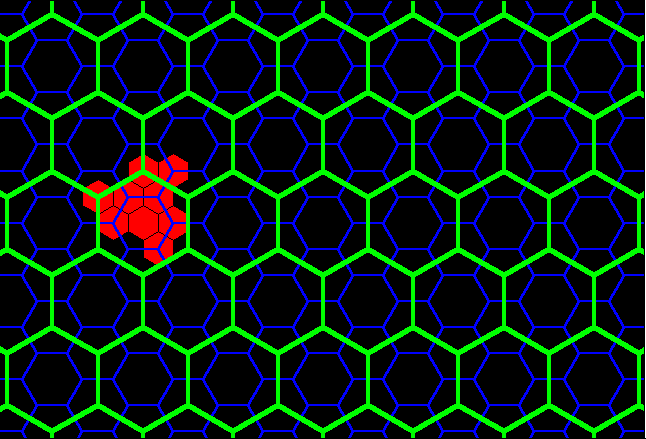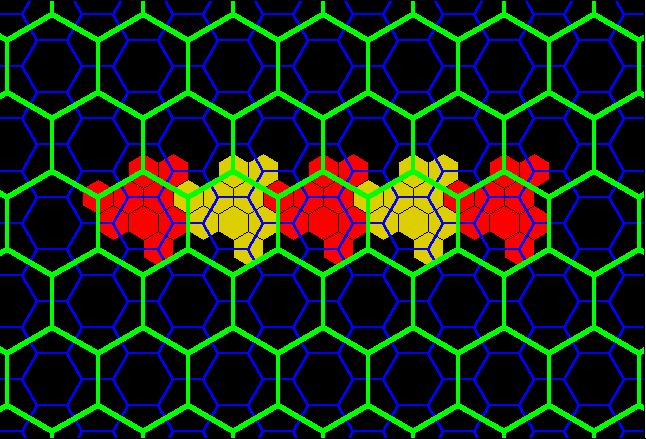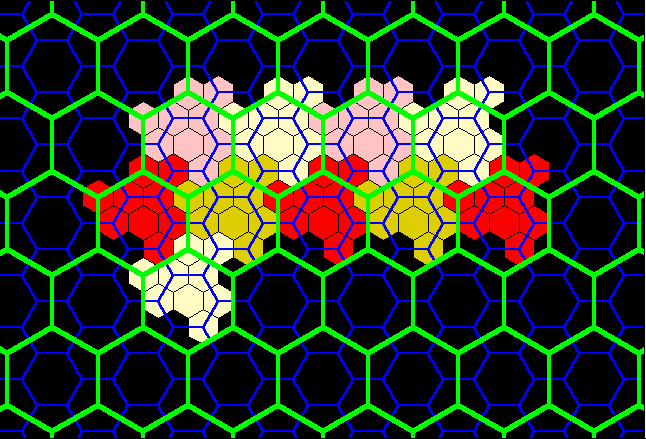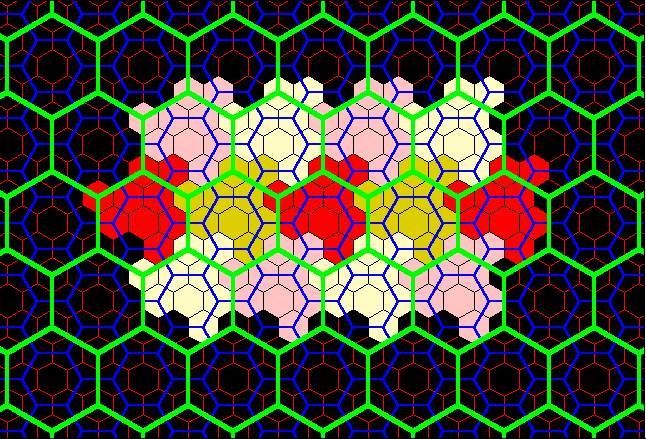Figure 13.  Red layer on tile from Figure 12 fits exactly to form classical K=3 landscape.  Note, that for contrast in blocks, the red layer from Figure 12 is alternately colored in shades of yellow, also.

Figure 14a.  Animated K=4 fractal iteration sequence:  first transformation using a three-sided fractal generator applied successively to sides of the hexagonal initiator.

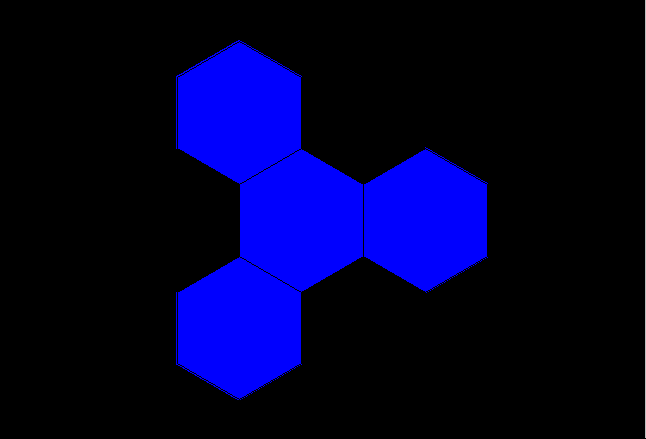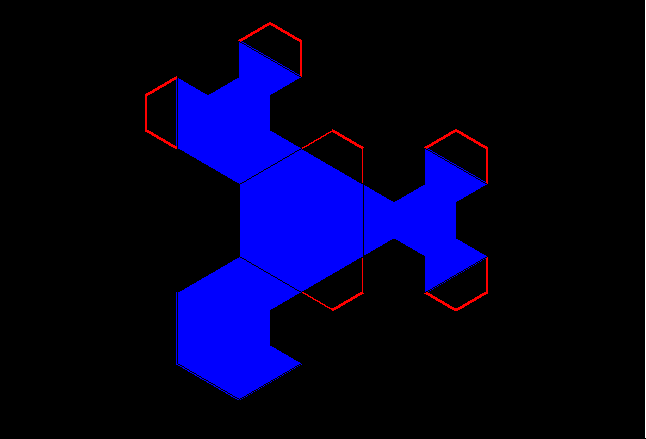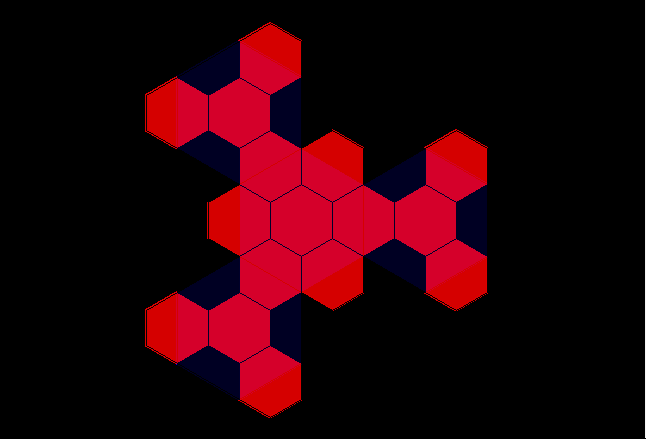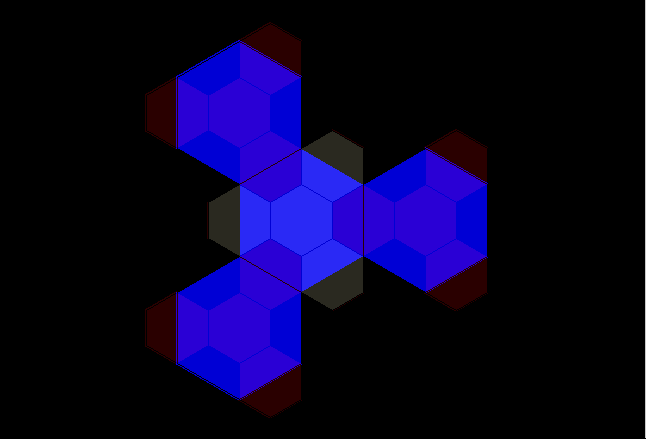
Figure 14b.  Animated K=4 fractal iteration sequence:  second transformation using a scaled-down three-sided fractal generator applied successively to sides of the blue polygon generated in Figure 14a.

Figure VR04.  A screen shot from the virtual world linked to this image.  Click on the image to enter that world!

Figure VR05.  A screen shot from the virtual world linked to this image.  Click on the image to enter that world!  Translucent solids permit one to see relationships among layers of the hexagonal hierarchy while travelling through the solids.

Figure 15.  Fractally generated layers stacked on a single hexagonal tile.  Click here to see a virtual solid model of the tile with which the reader can interact.  Click here to see a virtual translucent model of the tile with which the reader can interact.

     Finally, we tile the plane using the hexagonal initiators to discover if the superimposed structure also fits together perfectly (Figure 16).  Hexagonal tiles are used to cover the plane without gaps, as is the case with the sample of green hexagons in Figure 16a.  The hexagons mesh perfectly to cover the plane (Theorem of Gauss).  In Figure 16b, the green outline of the hexagons remains.  Each of the solid green hexagons has had the fractal generator above applied and the consequent superimposed blue tiles come into view sequentially in this animation.  Again, the fit is exact, as we had hoped it might be.  Finally, in Figure 16c, the blue outline only is retained from Figure 16b (along with the green outline from Figure 16a).  The final fractally generated layer derived from the blue polygons of Figure 16b comes into view in shades of red (or yellow/gold for contrast).  The final layer of hexagonal base of unit hexagons appears last.  The fit is perfect:  each green hexagon contains the equivalent of four blue hexagons and each blue hexagon contains the equivalent of four red hexagons.  The fractal generation procedure created exactly the classical central place landscape of Figure 5.   As the animation proceeds in Figure 16, further layers of the fractally generated hierarchy, attached to the tile in Figure 15, come into view illustrating an exact meshing of tiles at all levels to form a K=4 hierarchy.
 

Figure 16a.  Green layer on tile from Figure 15 fits exactly to tile the plane (Theorem of Gauss).

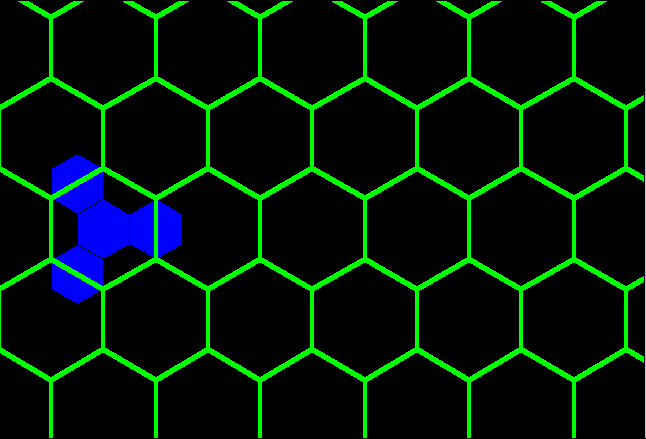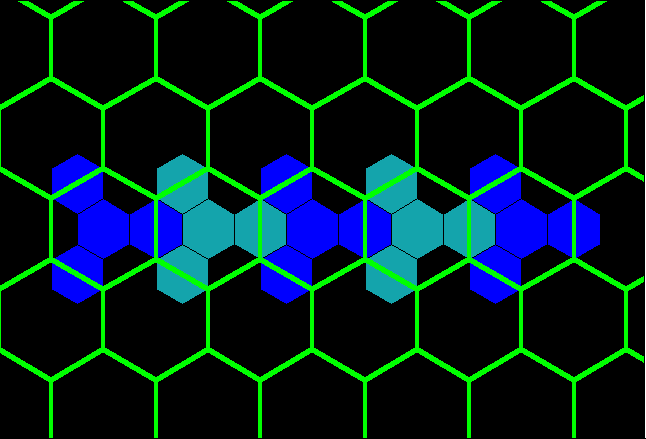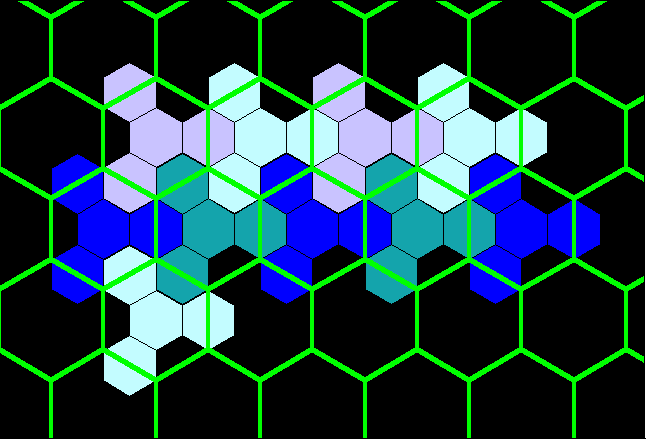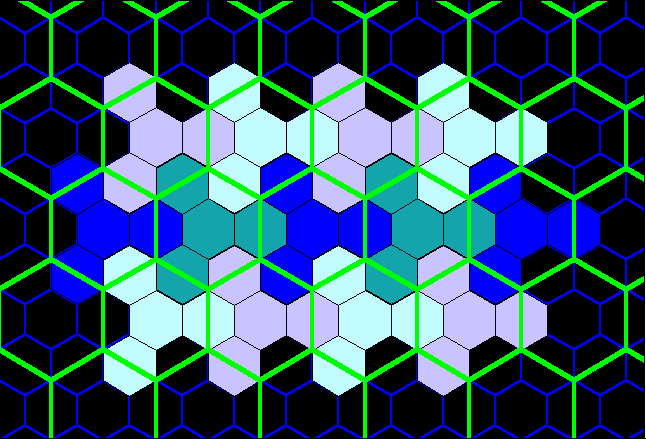Figure 16b.  Blue layer on tile from Figure 15 fits exactly to form classical K=4 landscape.

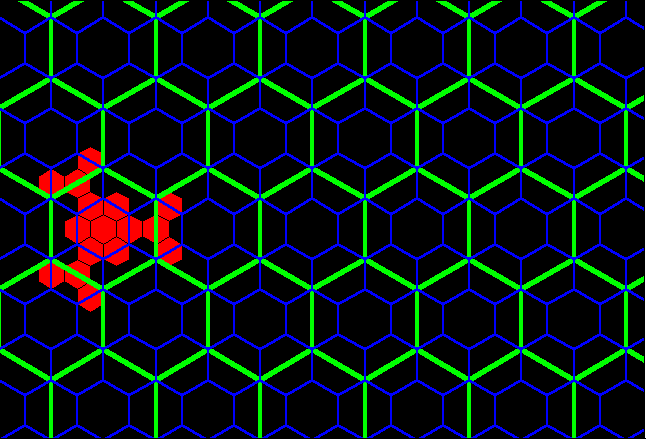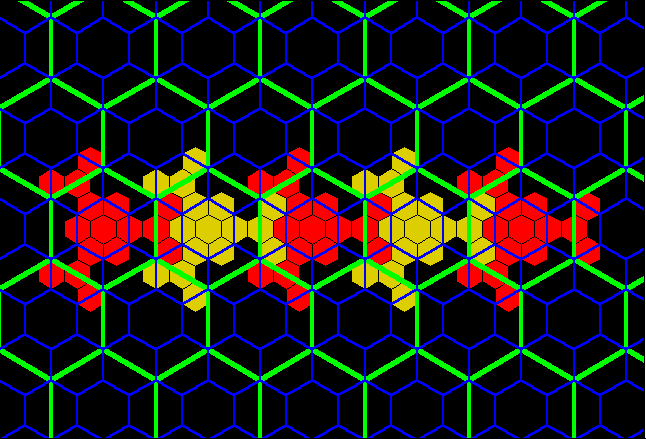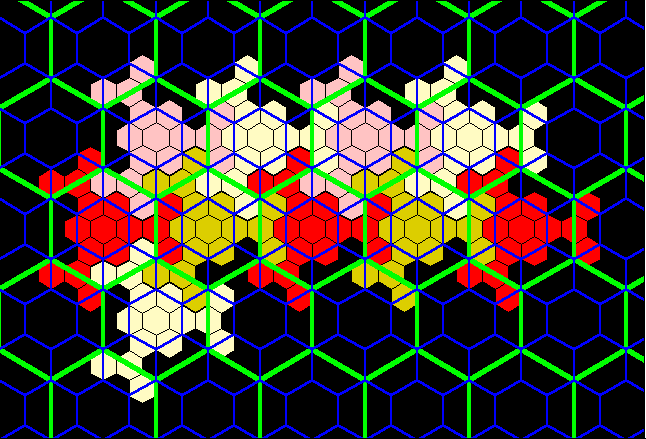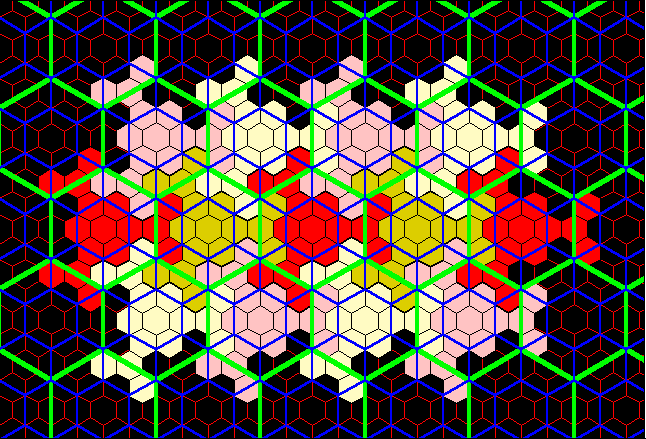Figure 16c.  Red layer on tile from Figure 15 fits exactly to form classical K=4 landscape.  Note, that for contrast in blocks, the red layer from Figure 15 is alternately colored in shades of yellow, also.

Figure 17a.  Animated K=7 fractal iteration sequence:  first transformation using a three-sided fractal generator applied successively to sides of the hexagonal initiator.

Figure 17b.  Animated K=7 fractal iteration sequence:  second transformation using a scaled-down three-sided fractal generator applied successively to sides of the blue polygon generated in Figure 17a.

Figure VR06.  A screen shot from the virtual world linked to this image.  Click on the image to enter that world!

Figure VR07.  A screen shot from the virtual world linked to this image.  Translucent solids permit one to see relationships among layers of the hexagonal hierarchy while travelling through the solids.  Click on the image to enter that world:  blast off in this virtual hexagonal space ship!

Figure 18.  Fractally generated layers stacked on a single hexagonal tile.  Click here to see a virtual solid model of the tile with which the reader can interact.  Click here to see a virtual translucent model of the tile with which the reader can interact.

Figure 19a.  Green layer on tile from Figure 18 fits exactly to tile the plane (Theorem of Gauss).

Figure 19b.  Blue layer on tile from Figure 18 fits exactly to form classical K=7 landscape.

Figure 19c.  Red layer on tile from Figure 18 fits exactly to form classical K=7 landscape.  Note, that for contrast in blocks, the red layer from Figure 18 is alternately colored in shades of yellow, also.

The Added Role of the Fractional Dimension
     A fractal iteration sequence, such as those above but carried out infinitely, might be thought to increase the extent to which a line "fills" space.  Both a single line segment and the letter "N" have Euclidean dimension 1; yet one of them fills more space than does the other.  Mandelbrot (and others before him) captures this notion of space-filling with the concept of fractional dimension (hence "fractal").  He uses Hausdorff-Besicovitch dimension to measure the enduring mathematical concept of space-filling.  We employ Mandelbrot's formulation for fractional dimension D as, D=log(number of generator sides)/log(square root of K).  Thus, the following values for fractally-generated central place hierarchies emerge:

• K=3, D=log2/log = 1.2618595
• K=4, D=log3/log 2    = 1.5849625
• K=7, D=log3/log = 1.1291501

    What is difficult with fractals is to visualize the infinite process.  Graphic color display, including three dimensional display, offers exciting strategies for visualization.  Very quickly, however, it becomes difficult to draw the fine lines required by repeating the process at more and more local scales:  lines have width.  Electronic lines can be controlled and made finer than can pen lines, but eventually the line-width limits the capability to produce graphic images.  Eventually, the mind's eye must take over and extrapolate the visual infinite process.
    Another possibility might be to draw on the other human senses to aid in that extrapolation.  Thus, Figure 20 shows figures generated by Fractal Music 1.9; click on the images and hear the associated music. The left figure shows the cellular automata base generated by default--it is bilaterally symmetric about a central vertical line and was generated using a symmetrically arranged initiator string of 64 digits ranging in value from 0 to 7 (one for each tone).  The next figure, K=3, shows the cellular automata diagram (another sort of "bubble foam" in appearance) generated using the value for the fractional dimension of the K=3 hexagonal hierarchy carried out to 64 decimal places as the initiator string for the music.  The next figure, K=4, shows the cellular automata diagram generated using the value for the fractional dimension of the K=4 hexagonal hierarchy carried out to 64 decimal places as the initiator string for the music.  The final figure, K=7, shows the cellular automata diagram generated using the value for the fractional dimension of the K=7 hexagonal hierarchy carried out to 64 decimal places as the initiator string for the music.  Click on each figure to hear the music.  Each musical sequence, of over 1000 steps, was created from the default base, changing only the initiator string, so that the fractional dimension is what operates on a "seed" value of basic notes.  The listener should hear the basic pattern in all characterizations:  great symmetry in the base value; abrupt changes of state in the K=3 value; a smoother filling of musical space in the K=4 music; and, gaps in the K=7 musical characterization derived from the K=7 fractional dimension.  Thus, we extend visualization from two dimensional graphical images to three dimensional graphical images to the mind's eye, and finally, to the mind's ear:  capturing hierarchical pattern through 1000 steps or more is easy in the musical clips. Such characterization offers added capability to those of us with all of our senses that are functional:  for those with limited visual sensory function, it offers a way to an auditory "visualization" of the beauty of geometry.

Base

K=3

K=4

K=7

    The complex mechanics of the theory behind hexagonal hierarchies come alive as a single dynamic system when visualized through the lens of fractal geometry.  The fit of the classical and fractal geometric hierarchies is exact.  Thus, as one might use a carefully surveyed topographic map, with field-checked spot elevations, as a guide into dense jungle or other unsurveyed landscapes, so too we use our carefully surveyed alignment of the classical and the fractal hexagonal hierarchies as a guide into unseen or unproven areas of geometry and geography.  The difference is that the "field" tests in one case occur "terrestrial space" while in the other the "field" tests occur in "geometry, number theory, and pure mathematics."

In the material above, we saw hexagonal hierarchies, of different orientation, cell size, and stacking characteristics, arise from the same base of unit hexagons.  These were associated with three integers:  3, 4, and 7.  The thoughtful reader might naturally ask a number of questions, such as:

• are there other numbers that would serve as K values or are 3, 4, and 7 the only such values?
• are 5 or 6 possible K values?
• are there K values larger than 7?
• how many K values are there?
• How does one determine the number of sides in a fractal generator that will generate a correct hierarchy for arbitrary K values?
• How does one determine fractal generator shape that will generate a correct hierarchy for arbitrary K values?

The result of Loeb/Dacey is important because it shows

• that there are an infinite number of possible K values
• that this infinity of values is in one-to-one correspondence with the integral lattice points in the plane
• that one can give a numerical generating function to create K values

Figure 21.  The coordinatized lattice points in yellow transform into K-values in cyan using the Diophantine equation K=x2+xy+y2

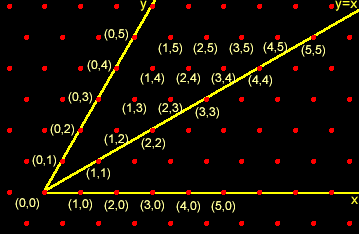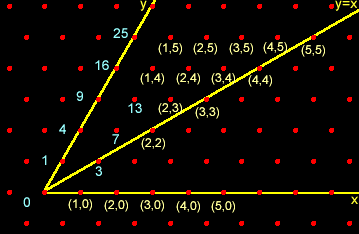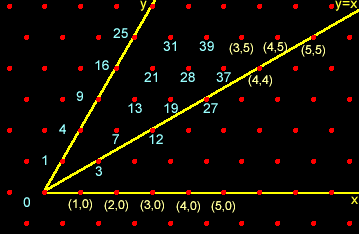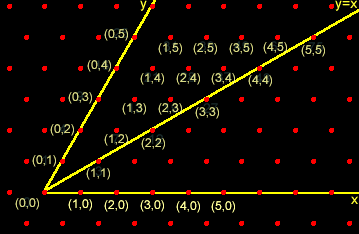Previous published research by the authors of this presentation has shown how to determine the number of sides in a fractal generator that will generate a correct hierarchy for arbitrary K values and
how to determine fractal generator shape that will generate a correct hierarchy for arbitrary K values.  Work in progress shows how to extend the three dimensional and other visualization schemes shown here to higher K values.  In it, we offer mathematical proof of these ideas and extensions of them into new realms.  The classical is used for alignment of new with the old:  a strategy useful in a wide range of theoretical and applied research.

1. Arlinghaus, Sandra L. 1985.  "Fractals take a central place," Geografiska Annaler, 67B, pp. 83-88. Journal of the Stockholm School of Economics.
2. Arlinghaus, Sandra Lach.  1990.  "Fractal geometry of infinite pixel sequences: `Super-definition' resolution?" Solstice:  An Electronic Journal of Geography and Mathematics, Institute of Mathematical Geography (the journal Solstice was in the Pirelli top 80, semi-finalist, in 2001)
3. Arlinghaus, Sandra Lach.  1993.  "Microcell Hex-nets?"  Solstice:  An Electronic Journal of Geography and Mathematics, Institute of Mathematical Geography
4. Arlinghaus, Sandra Lach. 1993.   "Electronic Geometry," The Geographical Review April, Vol. 83, No. 2, pp. 160-169.
5. Arlinghaus, Sandra Lach.  1993.  "Central Place Fractals"--Chapter 10 in Fractals in Geography, edited by Nina Lam and Lee DeCola, Prentice-Hall.
6. Arlinghaus, Sandra L. and Arlinghaus, William C.  1989.  "The fractal theory of central place hierarchies: a Diophantine analysis of fractal generators for arbitrary Löschian numbers," Geographical Analysis: an International Journal of Theoretical Geography. Ohio State University Press. Vol. 21, No. 2, April, pp. 103-121.
7. Arlinghaus, Sandra L. and Arlinghaus, William C. 2002,  Spatial Synthesis:  A Research Program, Solstice:  An Electronic Journal of Geography and Mathematics,  Volume XIII,  Number 2.
8. Arlinghaus, Sandra L. and Arlinghaus, William C.  2003.  Spatial Synthesis, Volume I, Book 1.  Forthcoming.
9. Arlinghaus, Sandra L., Arlinghaus, William C., and Harary, Frank.  Graph Theory and Geography:  An Interactive View eBook (Pirelli top 20, finalist, 2002), John Wiley and Sons, New York, 2002.
10. Boys, C. Vernon. 1902.  Soap Bubbles and the Forces which Mould Them. Society for Promoting Christian Knowledge.
11. Christaller, Walter. Struktur und Gestaltung der Zentralen Orte des Deutschen Ostens, Gemeinschaftswerk im Auftrage der Reichsarbeitsgemeinschaft für Raumforschung, Teil 1, Dr. Walter Christaller, Die Zentralen Orte in den Ostgebieten und ihre Kultur- und Marktbereiche, K. F. Koehler Verlag, Leipzig, 1941
12. Christaller, Walter. 1933.  Die zentralen Orte in Süddeutschland. Jena: Gustav Fischer. (Translated (in part), by Carlisle W. Baskin, as Central Places in Southern Germany. Prentice Hall 1966).
13. Coxeter, H. S. M. 1961. Introduction to Geometry.  New York:  John Wiley & Sons, pp. 53-54.
14. Dacey, Michael F.  The geometry of central place theory. Geografiska Annaler, B, 47, 1965, 111-124.
15. Fejes-Toth, Laszlo.  1968. Solid circle-packings and circle-coverings, Studia Sci. Math. Hungar. 3(1968).
16. Gauss, Carl Friedrich.  1840.  Untersuchungen über die Eigenschaften der positiven ternären quadratischen Formen von Ludwig August Seber, Göttingische gelehrte Anzeigen, Juli 9 [J. Reine Angew. Math. 20 (1840), 312-320:  Werke, Vol. 2 (Königlische Gesellschaft der Wissenschaften, Göttingen 1876), 188-196].
17. Kolars and Nystuen, 1974. Human Geography, New York:  McGraw-Hill.
18. Loeb, Arthur L. 1976.  Space Structures:  Their Harmony and Counterpoint.  Reading, MA:  Addison-Wesley.
19. Lösch, August. 1954.  The Economics of Location, translated by William H. Woglom.  New Haven:  Yale University Press.
20. Mandelbrot, Benoit.  1983.  The Fractal Geometry of Nature.  San Francisco:  W. H. Freeman.
21. Nystuen, J., 1966.  "Effects of boundary shape and the concept of local convexity;"  Michigan Interuniversity Community of Mathematical Geographers (unpublished).  Reprinted, Ann Arbor:  Institute of Mathematical Geography.
22. Singer, David H. 2003.  Fractal Music, 1.9, The Fractal Music Generator
23. Tufte, E. R.  (1990). Envisioning Information.  Cheshire, CT.  Graphics Press.
24. Vries, Hugo de.  1906.  Species and Varieties: Their Origin by Mutation (second edition; Chicago: The Open Court Publishing Company), ed. by Daniel Trembly MacDougal (Gutenberg text)