SOLSTICE: AN ELECTRONIC JOURNAL OF GEOGRAPHY AND MATHEMATICS.
Volume VII, Number 2. Winter, 1996.
SOLSTICE:
AN ELECTRONIC JOURNAL OF GEOGRAPHY AND MATHEMATICS
http://www-personal.umich.edu/~sarhaus/image
WINTER, 1996
VOLUME VII, NUMBER 2
ANN ARBOR, MICHIGAN
----------------------------------------------------------------------------
Founding Editor-in-Chief:
Sandra Lach Arlinghaus, University of Michigan;
Institute of Mathematical Geography (independent)
Editorial Advisory Board:
Geography.
Michael F. Goodchild, University of California, Santa Barbara
Daniel A. Griffith, Syracuse University
Jonathan D. Mayer, University of Washington (also School of Medicine)
John D. Nystuen, University of Michigan
Mathematics.
William C. Arlinghaus, Lawrence Technological University
Neal Brand, University of North Texas
Kenneth H. Rosen, A. T. & T. Bell Laboratories
Engineering Applications.
William D. Drake, University of Michigan
Education.
Frederick L. Goodman, University of Michigan
Business.
Robert F. Austin, Austin Communications Education Services.
Technical Editor:
Richard Wallace, University of Michigan.
Web Consultant:
William E. Arlinghaus, UMI
WebSite: http://www-personal.umich.edu/~sarhaus/image
Electronic address: sarhaus@umich.edu
------------------------------------------------------------------------------
MISSION STATEMENT
The purpose of Solstice is to promote interaction between geography
and mathematics. Articles in which elements of one discipline are used to
shed light on the other are particularly sought. Also welcome are
original contributions that are purely geographical or purely
mathematical. These may be prefaced (by editor or author) with commentary
suggesting directions that might lead toward the desired interactions.
Individuals wishing to submit articles or other material should contact an
editor, or send e-mail directly to sarhaus@umich.edu.
------------------------------------------------------------------------------
SOLSTICE ARCHIVES
Back issues of Solstice are available on the WebSite of the Institute
of Mathematical Geography, http://www-personal.umich.edu/~sarhaus/image
and on the GOPHER of the Arizona State University Department of
Mathematics. Thanks to Bruce Long for taking the initiative in this
matter. The connections to this GOPHER are available along a variety of
routes through the Internet.
------------------------------------------------------------------------------
PUBLICATION INFORMATION
The electronic files are issued yearly as copyrighted hardcopy in the
Monograph Series of the Institute of Mathematical Geography. This
material will appear in Volume 21 in that series, ISBN to be announced.
To order hardcopy, and to obtain current price lists, write to the
Editor-in-Chief of Solstice at 2790 Briarcliff, Ann Arbor, MI 48105, or
call 313-761-1231.
Suggested form for citation: cite the hardcopy. To cite the
electronic copy, note the exact time of transmission from Ann Arbor, and
cite all the transmission matter as facts of publication. Any copy that
does not superimpose precisely upon the original as transmitted from Ann
Arbor should be presumed to be an altered, bogus copy of Solstice.
------------------------------------------------------------------------------
TABLE OF CONTENTS, VOL. VII, No. 2.
1. WEB FRACTALS: AN OVERVIEW. Sandra Lach Arlinghaus.
2. PART II. ELEMENTS OF SPATIAL PLANNING: THEORY.
MERGING MAPS: NODE LABELING STRATEGIES
Sandra Lach Arlinghaus
3. INDEX TO SOLSTICE, VOLUME I (1990) TO THE PRESENT.
--------------------------------------------------------------------------------
1.
WEB FRACTALS: AN OVERVIEW
Sandra Lach Arlinghaus
The University of Michigan
Documents written in HTML (Hyper-Text Markup Language) for
WebSites not only offer the capability to place Home Pages on the World
Wide Web, but also extend the dimension in which typesetting takes place.
Broadly viewed, from a typesetting standpoint, HTML appears to be
equivalent to a subset of commands of Plain TeX. One notable exception
arises, however, in the commands in HTML that enable the user to specify
links to other documents, graphical or textual. A Home Page, or any other
page or set of pages (paper or electronic), might be viewed as a one
dimensional string of letters broken into words. Graphics offer an
opportunity to extend the text into other dimensions. So too do the links
from one web page to another. They offer an extraordinary capability to
reach out within the text itself: an opportunity to "fill" a text-shed
beyond the linear text-stream. Of course, one can mix and match links,
graphics, text, and whatever is available on the web. Without loss of
generality, interest might be confined to text because it is with text
that the extension into extra dimensions appears straightforward.
Thus, it becomes of interest to ask how much of a text-shed is
filled by the activity of creating links and how one might measure such
filling of text-space. Concepts from fractal geometry and from chaos
theory might be employed to consider these issues.
GLOBAL WEB VIEW
The global perspective employed in much of modern mathematics
focuses not on the individual objects being studied but on the sets of
transformations that enable one to move from one object, or type of
object, to another. Thus, one learns group theory by studying the various
morphisms that link groups, rather than by focusing on the tables that
describe individual groups. Linkages expose structure.
Thus, one view of the Web would be to shrink to nodes all home
pages and focus only on the links that exist between sites. The set of
nodes is finite, but it is unbounded--one can imagine going beyond any
upper bound on the number of sites, simply by adding one more. The set of
links, too, is finite and unbounded. The morass of links defies good
graphical description. Search engines try to make sense of the Web
through various organizational schemes. One view of the pattern is as a
cataloguerAs nightmare; another is as a chance to introduce order into
seeming abstract chaos.
Yet another might be to engage in graphical analysis based on some
sort of ordering scheme that permits the assessment of extent of space
filled. The concept of attractors and repellers seems an important one to
search engines. One such ordering scheme might be such as suggested
below. Of course there are many others, too.
y equals x means link...both to and from me to you
y greater than x means link...me to you
y less than x means link...me from you
The algebraic, geometric, and topological structure of the web are
important to analyze: the space-filling ideas represented in fractal
geometry suggest one style of approach. Any deep, careful mathematical
analysis should, however, offer a systematic means to evaluate the current
status of web content, and more important, provide a continuing framework
in which to guide and understand web development. These comments offer
mere hints at directions substantive work might take; hopefully, they
offer encouragement to consider the web itself as a source of various
styles of research opportunity.
Ann Arbor, MI
May, 1996
---------------------------------------------------------------------------------------------------------
2.
PART II. ELEMENTS OF SPATIAL PLANNING: THEORY.
MERGING MAPS: NODE LABELING STRATEGIES
Sandra Lach Arlinghaus
The University of Michigan
Different inventories of roads produce different maps; two
different maps can represent one set of actual roads. How is a planner to
rectify this situation? To consider the problem abstractly, it is useful
to characterize the road network as a graph, composed of nodes and edges
joining nodes. Such style of consideration, as a graphical puzzle, dates
from 1736 and the Konigsberg Bridge puzzle and from Hamilton's "Around the
World" puzzle of 1859 (Harary, pp. 1, 4); as a planner's dilemma it has no
doubt always been with us; and, as a cartographer's delight, it manifests
itself over and over again in projection selection, a result of the
one-point compactification theorem (visualized as stereographic
projection) forcing us to recognize that the sphere can never be flattened
out into the plane.
In Figure 1, two portions of road maps based loosely on the
downtown Ann Arbor, Michigan, street map are shown superimposed--a
conceptual view of a practical problem noted by John Nystuen, and
implemented at the level of mapping by Andrea Frank and Jyothi
Palathinkara (University of Michigan). As Nystuen et al. noted
(unpublished communication), these nodes are, in some sense at least,
fairly "close"--one can recognize, visually, what the correspondence is to
be from one map to the other. The viewpoint adopted here is that as
graph-theoretic trees they are homeomorphic (have the same structure or
connection pattern).

Figure 1. Two trees representing the same actual street pattern.
If the planners who use these maps rely on a node labeling scheme,
in which both maps are labeled from the top down, beginning in the upper
left hand corner, proceeding horizontally and then in a serpentine pattern
from top to bottom, the first node encountered is labeled with the numeral
1; the second node encountered is labeled with the numeral 2, and so forth
(Figure 2). However, the labeling imposed on these two maps is not
identical, as one would wish (to indicate their identity in topological
form). Indeed, the label 3 on the red tree then corresponds to the label
4 on the black tree and vice-versa, as do labels 5 and 6; a situation
Nystuen et al. noted and were able to uncover on a number of occasions on
actual maps (Figure 2). Naturally, as they note, one would wish, in a
situation such as this one, to have the numerals correspond in an
appropriate manner.
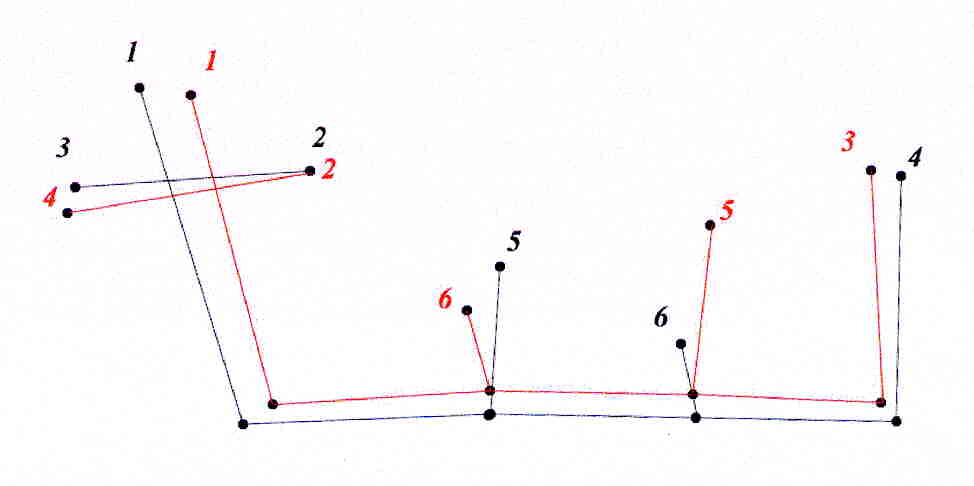
Figure 2. The red route and the black route: numbered nodes do not
correspond as desired. The numbering scheme is a common one in which
nodes are labeled from the top down in a left/right serpentine pattern
(after Nystuen et al.).
Nystuen's observation came from a real-world example; it points,
once again, to the appropriateness of considering different labeling
schemes that will permit alignment of maps based on topology rather than
solely on distance from the top of the screen. One strategy, that takes
advantage of the structure of the underlying raster on which these maps
were produced, proceeds as follows.
CANTOR PIXEL-LABELING ALGORITHM
1. Designate as a fundamental screen unit the smallest dot size
to be used to represent a node; without loss of generality it can be
assumed to be a "pixel."
2. In the manner that has come to be conventional with cathode
ray tubes, use the top of the screen as the positive x-axis and the left
side of the screen as the positive y-axis (with origin at the upper
left-hand corner of the screen).
3. Assign to each pixel on the CRT an ordered pair of Cartesian
coordinates: (1,2) is a pixel (an indivisible area) located one unit to
the right of the left edge of the screen and two units down from the top.
4. Assign to each node in one map the pixel coordinates of the
node as follows. If the pixel coordinates are (x,y), label the node with
the rational number y/x.
This sort of strategy differs from what may be a computer default
labeling scheme. Each possible node location has a unique label that is a
single rational number indicating pixel location referred both to raster
position and to location in relation to other pixels. The serpentine
labeling scheme is still preserved even though its form is different, and
perhaps, not evident. Cantor's enumeration technique shows that there is
a one-to-one correspondence between the set of natural numbers and the set
of ordered pairs of natural numbers. These two sets have the same
cardinal number, aleph null (Hahn, pp. 1595-1596). Cantor's serpentine
pattern through a square lattice converts the two-dimensional array into a
one dimensional stream clearly equivalent to a number line (Figure 3).

Figure 3. Assignment scheme for illustrating the cardinality of the set
of rational numbers (after Hahn, p. 1595).
This strategy was the basis for Georg Cantor's (perhaps
counter-intuitive) proof that the cardinal number of the set of rational
numbers is aleph null. The set of ordered pairs contains the set of
rationals--for, when ordered pairs are converted to rationals, as in the
algorithm above, some are equivalent in value although not in visual
form--1/2 and 2/4 are equivalent in value but do not look the same.
However, the rational numbers contain the natural numbers as a subset.
Thus, the cardinal number of the rationals is sandwiched between two sets
each of whose cardinal number is aleph null--consequently, the set of
rational numbers must also have cardinal number aleph null. Thus, the set
of numbers y/x exactly covers the screen.
REPETITION OF THE CANTOR ALGORITHM
Suppose that the Cantor Algorithm has been applied once to a map:
to the red tree in Figure 2, for example. Each node of the red tree will
have a distinct, unique rational number label based on its position
relative to the top and the side of the screen and in relation to other
nodes. In a different layer, label the black street map in the same
manner. It appears that at most one node on these two maps will have the
same label; indeed, using rational number labeling, two nodes have the
same label if and only if they are represented by the same pixel location
in both maps. What is desired is to identify (match up or glue together)
a node from one map with a node from the other map both of which represent
the same physical location.
MERGING ALGORITHM
The following algorithm offers a strategy for making such an
identification. It can be executed by buffering nodes, in an iterative
fashion, and identifying two nodes at the first instance a node from one
map falls into a node-buffer in another map.
1. Draw a buffer of one pixel width around each node in the red
map. Assign identical labels to any pair of nodes on red and black maps
both of which lie within or on the buffer.
2. Draw a buffer of one pixel width around each buffered node
created in step 1. Assign identical labels to any pair of nodes on the
red and black maps both of which lie within or on this newly drawn ring
buffer region.
3. Repeat the process until one pair of buffer zones comes into
contact with each other. Then stop the process.
If this Merging Algorithm provides a complete identification of nodes
(with no extra nodes lying in the region outside the buffered zone), with
identical connection patterns in both, then the two maps are said to be
pairwise "well-matched." There is no difficulty in merging the two maps
from different sources.
TRANSLATION OF THE MERGING ALGORITHM
Maps may fail to be pairwise well-matched for a variety of
reasons. The following list suggests some reasons for such failure, but
it may not be exhaustive.
1. The numbers of nodes in the red and black maps are different from each
other.
2. The number of nodes in the two maps is the same, but the number of
edges is different.
3. The number of nodes and edges is the same in both maps but the
topology, the pattern of connection, is different.
4. Some or all of the three factors above may hold, in whole or in part,
but the offset of pattern is so large that it falls outside the would-be
buffer zone and gets visually confused with other pattern.
Nystuen notes in some of his examples that some parts of each map in the
pair are shifted; the structure is recognizable from one to the other, but
offset some significant amount. One way to deal with situations of these
sorts is to permit translation, locally, of parts of the graph in one map.
The Merging Algorithm will run in a satisfactory manner, up to a point.
Beyond this point, nodes fall outside buffer zones. In such situations,
use the diameter of the buffer zone (number of maximum number of pixels
that came about in the use of the Merging Algorithm) as a translation
scaling number. Add this number to each coordinate (in the local region)
in one map. Now run the Merging Algorithm. Repeat the procedure as
needed.
DIRECTIONS FOR FURTHER WORK
This issue of merging maps appears rich from an abstract
viewpoint. Some of the other directions one might consider involve use of
Hasse's Algorithm applied to graphs, development of error detection and
correction criteria, use of sum-graphs or a similar strategy in which the
topology of the graph guides the labeling pattern, and any of a host of
theorems related to these topics.
Ann Arbor, MI
April, 1996.
REFERENCES
Hahn, Hans. "Infinity" in The World of Mathematics, James R. Newman
(Ed.), New York: Simon and Shuster, 1956.
Harary, Frank. Graph Theory. Reading: Addison-Wesley, 1969.
Nystuen, John D. Personal communication, unpublished, 1996.
---------------------------------------------------------------------------------------------------------4.
INDEX TO VOLUMES I (1990) TO VOL. VI
--------------------
VOL. VII, NUMBER 1.
TABLE OF CONTENTS
1. PHOTO ESSAY
THE GREENING OF DETROIT, 1975-1992:
PHYSICAL EFFECTS OF DECLINE
John D. Nystuen, Rhonda Ryznar, Thomas Wagner
2. ALGEBRAIC ASPECTS OF RATIOS
Sandra Lach Arlinghaus
3. EDUCATION GRAPHIC ESSAY
U.S. ROUTE 12 BUFFER
Daniel Jacobs
4. INDEX TO VOLUMES I (1990) TO V (1995).
--------------------
Vol. VI, No. 2, December, 1995. TABLE OF CONTENTS
Elements of Spatial Planning: Theory--Part I.
Sandra L. Arlinghaus
MapBank: An Atlas of On-line Base Maps
Sandra L. Arlinghaus
International Society of Spatial Sciences
Volume VI, Number 1, June, 1995.
Fifth Anniversary of Solstice
New format for Solstice and new Technical Editor
Richard Wallace. Motor Vehicle Transport and Global Climate Change:
Policy Scenarios.
Expository Article. Discrete Mathematics and Counting Derangements in
Blind Wine Tastings.
Sandra L. Arlinghaus, William C. Arlinghaus, John D. Nystuen
--------------------
Volume V, No. 2, Winter, 1994.
Sandra L. Arlinghaus, William C. Arlinghaus, Frank Harary: The Paris
Metro: Is its Graph Planar?
Planar graphs; The Paris Metro; Planarity and the Metro;
Significance of lack of planarity.
Sandra Lach Arlinghaus: Interruption!
Classical interruption in mapping; Abstract variants on interruption
and mapping; The utility of considering various mapping surfaces--GIS;
Future directions.
Reprint of Michael F. Dacey: Imperfections in the Uniform Plane.
Forewords by John D. Nystuen.
Original (1964) Nystuen Foreword; Current (1994) Nystuen Foreword;
The Christaller spatial model; A model of the imperfect plane; The
disturbance effect; Uniform random disturbance; Definition of the basic
model; Point to point order distances; Locus to point order distances;
Summary description of pattern; Comparison of map pattern; Theoretical
model; Point to point order distances; Locus to point order distances;
Summary description of pattern; Comparison of map pattern; Theoretical
order distances; Analysis of the pattern of urban places in Iowa; Almost
periodic disturbance model; Lattice parameters; Disturbance variables;
Scale variables; Comparison of M(2) and Iowa; Evaluation; Tables.
Sandra L. Arlinghaus: Construction Zone: The Brakenridge-MacLaurin
Construction.
William D. Drake: Population Environment Dynamics: Course and
Monograph--descriptive material.
----------------------------
Volume V, No. 1, Summer, 1994.
Virginia Ainslie and Jack Licate: Getting Infrastructure Built.
Cleveland infrastructure team shares secrets of success;
What difference has the partnership approach made; How process
affects products--moving projects faster means getting more public
investment; difference has the partnership approach made; How process
affects products--moving projects faster means getting more public
investment; How can local communities translate these successes to their
own settings?
Frank E. Barmore: Center Here; Center There; Center, Center Everywhere.
Abstract; Introduction; Definition of geographic center; Geographic
center of a curved surface; Geographic center of Wisconsin; Geographic
center of the conterminous U.S.; Geographic center of the U.S.; Summary
and recommendations; Appendix A: Calculation of Wisconsin's geographic
center; Appendix B: Calculation of the geographical center of the
conterminous U.S.; References.
Barton R. Burkhalter: Equal-Area Venn Diagrams of Two Circles: Their
Use with Real-World Data
General problem; Definition of the two-circle problem; Analytic
strategy; Derivation of B% and AB% as a function of r(B) and d(AB).
Sandra L. Arlinghaus, William C. Arlinghaus, Frank Harary, John D.
Nystuen. Los Angeles, 1994 -- A Spatial Scientific Study.
Los Angeles, 1994; Policy implications; References; Tables and
complicated figures.
--------------------
Volume IV, No. 2, Winter, 1993.
William D. Drake, S. Pak, I. Tarwotjo, Muhilal, J. Gorstein, R. Tilden.
Villages in Transition: Elevated Risk of Micronutrient Deficiency.
Abstract; Moving from traditional to modern village life: risks
during transtion; Testing for elevated risks in transition villages;
Testing for risk overlap within the health sector; Conclusions and policy
implications
Volume IV, No. 1, Summer, 1993.
Sandra L. Arlinghaus and Richard H. Zander: Electronic Journals:
Observations Based on Actual Trials, 1987-Present.
Abstract; Content issues; Production issues; Archival issues;
References
John D. Nystuen: Wilderness As Place.
Visual paradoxes; Wilderness defined; Conflict or synthesis;
Wilderness as place; Suggested readings; Sources; Visual illusion authors.
Frank E. Barmore: The Earth Isn't Flat. And It Isn't Round Either:
Some Significant and Little Known Effects of the Earth's Ellipsoidal
Shape.
Abstract; Introduction; The Qibla problem; The geographic center;
The center of population; Appendix; References.
Sandra L. Arlinghaus: Micro-cell Hex-nets?
Introduction; Lattices: Microcell hex-nets; References
Sandra L. Arlinghaus, William C. Arlinghaus, Frank Harary:
Sum Graphs and Geographic Information.
Abstract; Sum graphs; Sum graph unification: construction;
Cartographic application of sum graph unification; Sum graph
unification: theory; Logarithmic sum graphs; Reversed sum graphs;
Augmented reversed logarithmic sum graphs; Cartographic application of
ARL sum graphs; Summary.
--------------------
Volume III, No. 2, Winter, 1992.
Frank Harary: What Are Mathematical Models and What Should They Be?
What are they?
Two worlds: abstract and empirical; Two worlds: two levels; Two
levels: derivation and selection; Research schema; Sketches of
discovery; What should they be?
Frank E. Barmore: Where Are We? Comments on the Concept of Center of
Population.
Introduction; Preliminary remarks; Census Bureau center of
population formulae; Census Bureau center of population description;
Agreement between description and formulae; Proposed definition of the
center of population; Summary; Appendix A; Appendix B; References.
Sandra L. Arlinghaus and John D. Nystuen: The Pelt of the Earth: An
Essay on Reactive Diffusion.
Pattern formation: global views; Pattern formation: local views;
References cited; Literature of apparent related interest.
Volume III, No. 1, Summer, 1992.
Harry L. Stern: Computing Areas of Regions with Discretely Defined
Boundaries.
Introduction; General formulation; The plane; The sphere; Numerical
examples and remarks; Appendix--Fortran program.
Sandra L. Arlinghaus, John D. Nystuen, Michael J. Woldenberg: The
Quadratic World of Kinematic Waves.
--------------------
Volume II, No. 2, Winter, 1991.
Reprint of Saunders Mac Lane: Proof, Truth, and Confusion, The Nora
and Edward Ryerson Lecture at The University of Chicago in 1982.
The fit of ideas; Truth and proof; Ideas and theorems; Sets and
functions; Confusion via surveys; Cost-benefit and regression;
Projection, extrapolation, and risk; Fuzzy sets and fuzzy thoughts;
Compromise is confusing.
Robert F. Austin: Digital Maps and Data Bases: Aesthetics versus
accuracy.
Introduction; Basic issues; Map production; Digital maps;
Computerized data bases; User community.
Volume II, No. 1, Summer, 1991.
Sandra L. Arlinghaus, David Barr, John D. Nystuen:
The Spatial Shadow: Light and Dark -- Whole and Part.
This account of some of the projects of sculptor David Barr attempts
to place them in a formal systematic, spatial setting based on the
postulates of the science of space of William Kingdon Clifford (reprinted
in Solstice, Vol. I, No. 1.).
Sandra L. Arlinghaus: Construction Zone--The Logistic Curve.
Educational feature--Lectures on Spatial Theory.
--------------------
Volume I, No. 2, Winter, 1990.
John D. Nystuen: A City of Strangers: Spatial Aspects of Alienation
in the Detroit Metropolitan Region.
This paper examines the urban shift from "people space" to "machine
space" (see R. Horvath, Geographical Review, April, 1974) in the Detroit
metropolitan regions of 1974. As with Clifford's Postulates, reprinted
in the last issue of Solstice, note the timely quality of many of the
observations.
Sandra Lach Arlinghaus: Scale and Dimension: Their Logical Harmony.
Linkage between scale and dimension is made using the Fallacy of
Division and the Fallacy of Composition in a fractal setting.
Sandra Lach Arlinghaus: Parallels Between Parallels.
The earth's sun introduces a symmetry in the perception of its
trajectory in the sky that naturally partitions the earth's surface into
zones of affine and hyperbolic geometry. The affine zones, with single
geometric parallels, are located north and south of the geographic
parallels. The hyperbolic zone, with multiple geometric parallels, is
located between the geographic tropical parallels. Evidence of this
geometric partition is suggested in the geographic environment--in the
design of houses and of gameboards.
Sandra L. Arlinghaus, William C. Arlinghaus, and John D. Nystuen: The
Hedetniemi Matrix Sum: A Real-world Application.
In a recent paper, we presented an algorithm for finding the
shortest distance between any two nodes in a network of n nodes when
given only distances between adjacent nodes (Arlinghaus, Arlinghaus,
Nystuen, Geographical Analysis, 1990). In that previous research, we
applied the algorithm to the generalized road network graph surrounding
San Francisco Bay. Here, we examine consequent changes in matrix entries
when the underlying adjacency pattern of the road network was altered by
the 1989 earthquake that closed the San Francisco--Oakland Bay Bridge.
Sandra Lach Arlinghaus: Fractal Geometry of Infinite Pixel
Sequences: "Super-definition" Resolution?
Comparison of space-filling qualities of square and hexagonal pixels.
Sandra Lach Arlinghaus: Construction Zone--Feigenbaum's number; a
triangular coordinatiztion of the Euclidean plane; A three-axis
coordinatization of the plane.
Volume I, No. 1, Summer, 1990.
Reprint of William Kingdon Clifford: Postulates of the Science of
Space.
This reprint of a portion of Clifford's lectures to the Royal
Institution in the 1870s suggests many geographic topics of concern in
the last half of the twentieth century. Look for connections to boundary
issues, to scale problems, to self-similarity and fractals, and to
non-Euclidean geometries (from those based on denial of Euclid's parallel
postulate to those based on a sort of mechanical `polishing'). What else
did, or might, this classic essay foreshadow?
Sandra Lach Arlinghaus: Beyond the Fractal.
The fractal notion of self-similarity is useful for characterizing
change in scale; the reason fractals are effective in the geometry of
central place theory is because that geometry is hierarchical in nature.
Thus, a natural place to look for other connections of this sort is to
other geographical concepts that are also hierarchical. Within this
fractal context, this article examines the case of spatial diffusion.
When the idea of diffusion is extended to see "adopters" of an
innovation as "attractors" of new adopters, a Julia set is introduced as
a possible axis against which to measure one class of geographic
phenomena. Beyond the fractal context, fractal concepts, such as
"compression" and "space-filling" are considered in a broader
graph-theoretic setting.
William C. Arlinghaus: Groups, Graphs, and God.
Sandra L. Arlinghaus: Theorem Museum--Desargues's Two Triangle
Theorem from projective geometry.
Construction Zone--centrally symmetric hexagons.
------------------------------------------------------------------------



