VISUAL TRIGONOMETRY REVIEW

Set screen to highest resolution; scroll to the right when needed.  The big table has four columns.
THE BASIC SETUP:

Unit circle, axis, and complementary (orthogonal) axis designated as co-axis.
Secant line, a geometric object, cuts the circle at an angle of theta to the horizontal axis. The secant line intersects the circle at point P.
The same secant line also determines the complementary angle to theta (another geometric object), denoted co-theta.
THE TOP ROW SHOWS DERIVATIONS OF TRIGONOMETRIC FUNCTIONS FOR ANGLE THETA;
THE SECOND ROW SHOWS DERIVATIONS OF TRIGONOMETRIC FUNCTIONS FOR ANGLE CO-THETA.

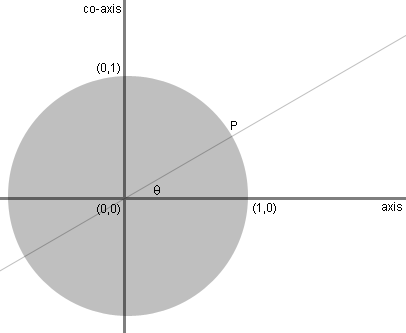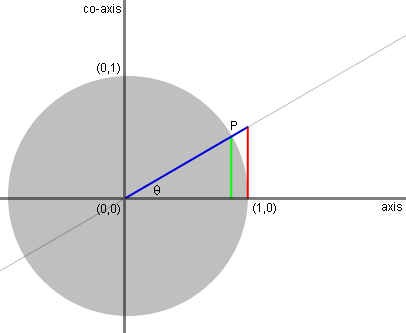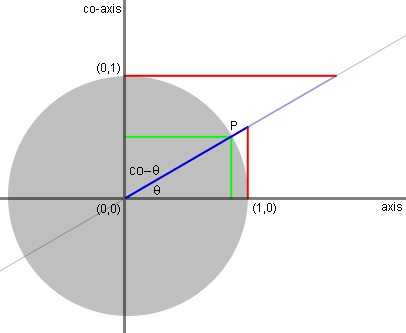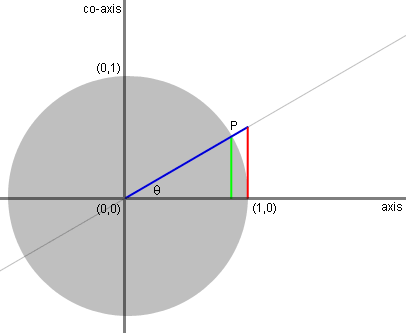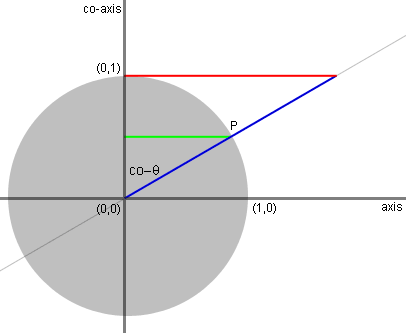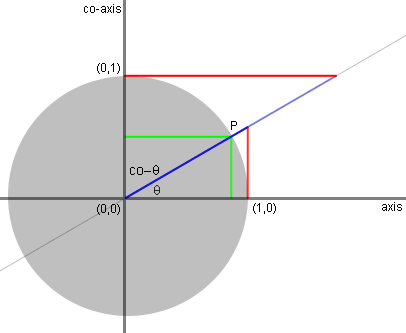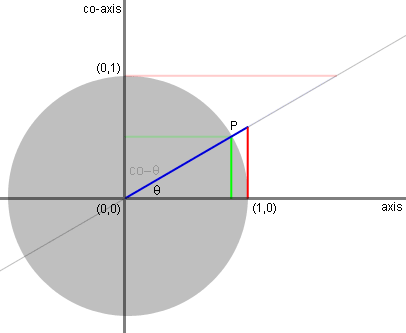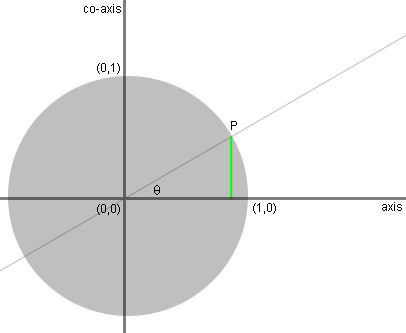
The length of the green line, dropping from P to the axis, measures the sine of theta:  opposite side of a right triangle over a hypotenuse of the unit circle.
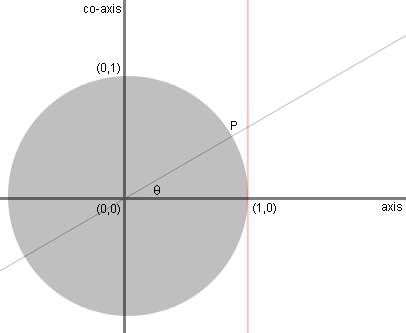
The pink line is a geometric line tangent to the unit circle at (1,0) on the horizontal axis.
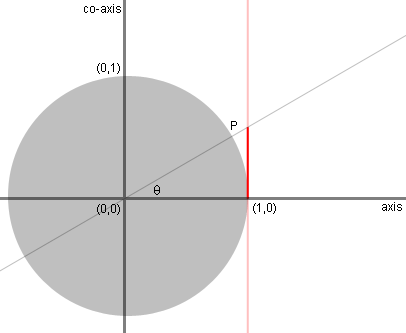
The length of the red line, intercepted by the secant line along the tangent line, measures the tanget of theta. 
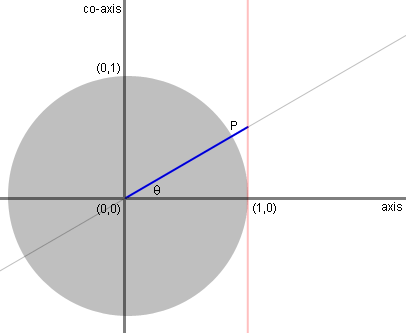
The length of the blue line, intercepted by the tangent line along the secant line, measures the secant of theta.

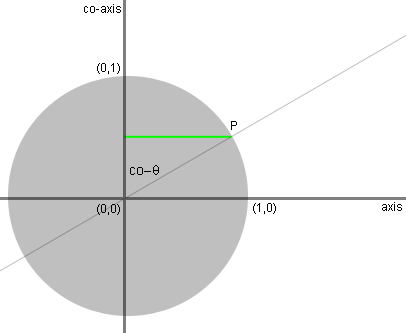
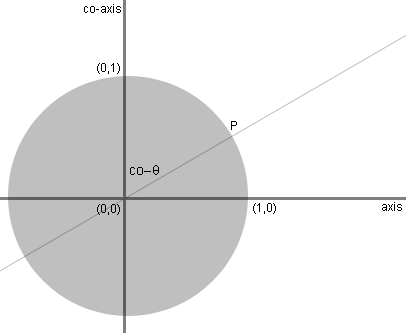
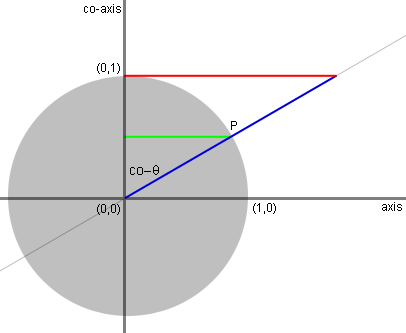
The length of the green line, dropping from P to the co-axis, measures the sine of co-theta:  opposite side of a right triangle over a hypotenuse of the unit circle.  Hence, cosine of theta.
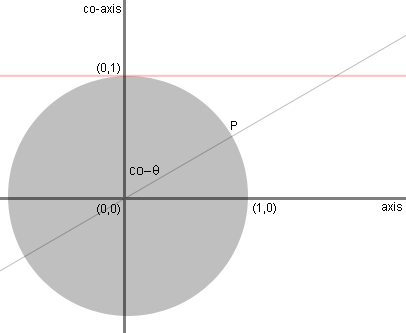
The pink line is a geometric line tangent to the unit circle at (1,0) on the co-axis.
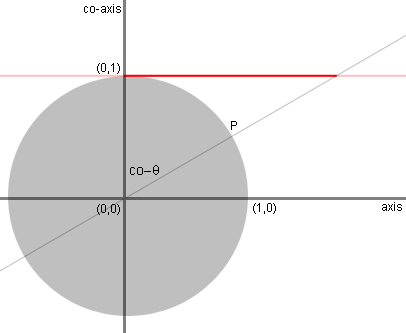
The length of the red line, intercepted by the secant line along the tangent line, measures the tanget of co-theta. Hence, cotanget of theta
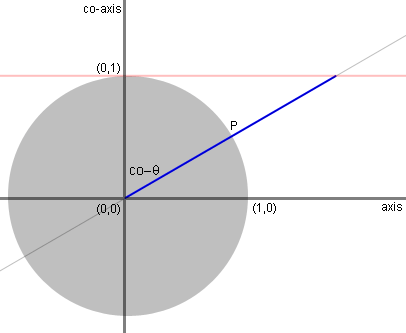
The length of the blue line, intercepted by the tangent line along the secant line, measures the secant of co-theta.  Hence, cosecant of theta.

 

The three functions of theta measuring sine, tangent, and secant shown together.
The three functions of co-theta measuring sine of co-theta (cosine of theta), tangent of co-theta (cotangent of theta), and secant of co-theta (cosecant of theta).
All six functions of theta are shown in this image.  The representations for secant lies on top of that for cosecant of theta.  The latter is thus shaded a lighter shade.

 
An animation of the ideas shown as individual frames above.

A number of trigonmetric identities are evident from this visual approach.

From the Pythagorean Theorem, it follows that:

sin2 theta + cos2 theta = 1, the radius of the unit circle measured along the secant line;
sec2 theta =  tan2 theta + 1, the radius of the unit circle measured along the horizontal axis;
csc2 theta = cot2 theta + 1, the radius of the unit circle measured along the co-axis.

What others do you note?

Based on an approach learned by S. Arlinghaus at The University of Chicago Laboratory Schools.

Copyright, S. Arlinghaus, 2004.