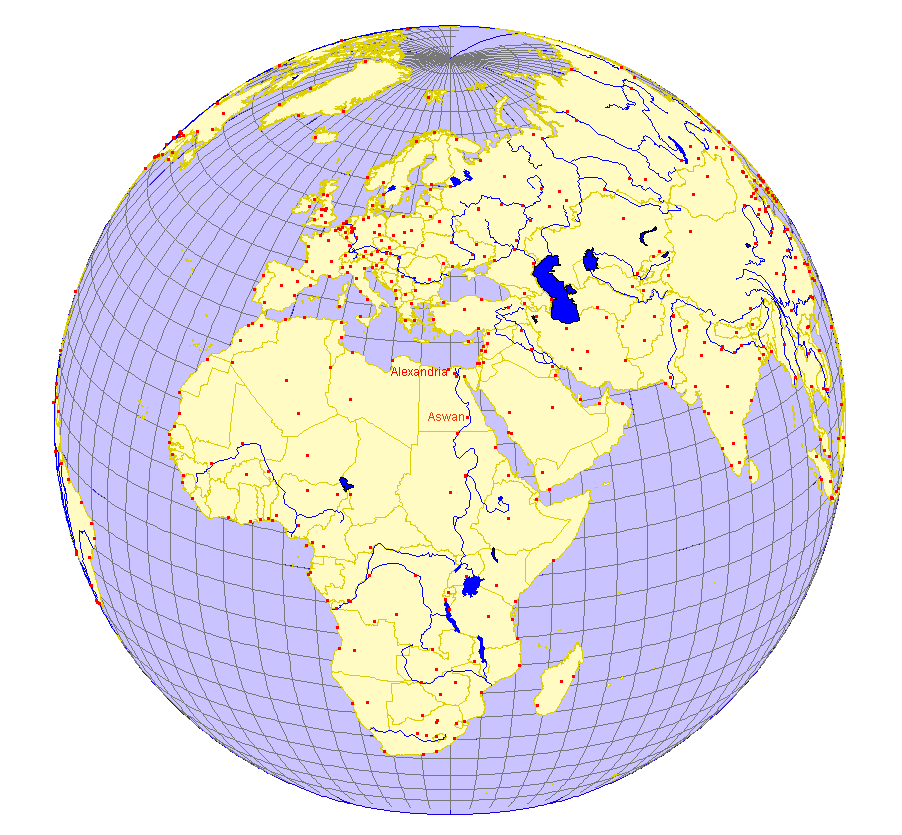
Figure 1. Relative location of Alexandria and Aswan. They are close to lying on the same meridian (half of a great circle). |

Figure 1. Relative location of Alexandria and Aswan. They are close to lying on the same meridian (half of a great circle). |
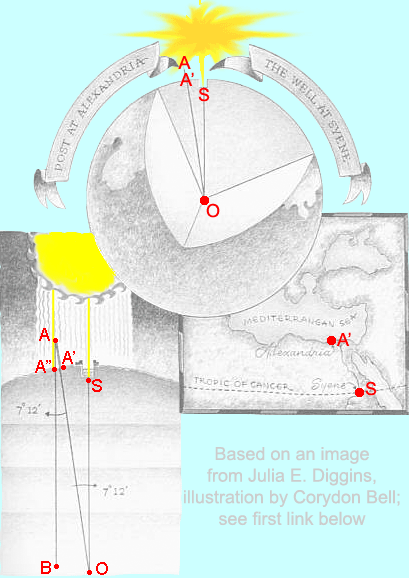
Figure 2. Eratosthenes's measurement of the circumference of the Earth, based on a Theorem of Euclid. |