Adaptive Mesh Refinement (AMR) techniques provide an attractive framework for atmospheric flows since they allow an improved resolution in limited regions without requiring a fine grid resolution throughout the entire model domain. The model regions at high resolution are kept at a minimum and can be individually tailored towards the research problem associated with atmospheric model simulations.
A solution-adaptive grid is a virtual necessity for resolving a problem with different length scales. In order to avoid under-resolving high-gradient regions in the problem, or conversely, over-resolving low-gradient regions at the expense of more critical regions, solution adaptation is a powerful tool saving several orders of magnitude in computing resources for many problems. Climate and weather models, or generally speaking computational fluid dynamics (CFD) codes, are among the many applications that are characterized by  multiscale phenomena and their resulting interactions.
For instance, large-scale weather systems such as midlatitude cyclones drive small-scale frontal zones, thunderstorms or rain events. These small-scale features may then influence the larger scale if, as an example, evaporation processes and turbulence at the surface trigger sensible and latent heat fluxes. But although today's atmospheric general circulation models (GCMs), and in particular weather prediction codes, are already capable of uniformly resolving horizontal scales of order 10-20 km (e.g. the model IFS of the European Centre for Medium-Range Weather Forecasts), the atmospheric motions of interest span many more scales than those captured in a fixed resolution model run. The widely varying spatial and temporal scales, in addition to the nonlinearity of the dynamical system, raise an interesting and challenging modeling problem. Solving such a problem more efficiently and accurately requires variable resolution.

Until 2008, our developments of an adaptive dynamical core for weather and climate research were based on the so-called Lin-Rood Finite-Volume (FV) dynamical core that had been designed at the NASA Goddard Space Flight Center (NASA/GSFC) in the late 1990's. This hydrostatic global dynamics package in flux form is built upon the Lin and Rood 1996 advection algorithm, which utilizes advanced oscillation-free numerical approaches to solving the transport equation. In particular,  Lin and Rood 1996 extended a Godunov-type methodology to multiple dimensions and made use of 2nd order van Leer-type (van Leer 1974, van Leer 1979) and 3rd order piecewise parabolic (PPM) methods (Colella and Woodward 1984, Carpenter et al. 1990). In 1997, the advection scheme became the fundamental building block of a shallow water code (Lin and Rood 1997, Lin 1997) which then led to the development of the current 3D, primitive-equation (PE) based, finite-volume dynamics package (Lin 2004) on a latitude-longitude grid.

Today (in 2016), the 3D FV dynamical core (lat-lon) and its newer cubed-sphere variant (FV3, dveloped at GFDL and NASA) is used operationally for data assimilation applications at NASA/GSFC, for weather and climate simulations at NOAA GFDL (and soon by NOAA's National Weather Service). Furthermore, the lat-lon FV dynamical core became part of NCAR's Community Earth System Model (CESM) in 2001. This climate prediction system contains the Community Atmosphere Model, CAM, with physics and dynamics components. In particular, the finite-volume dynamical core is now one of the four available dynamics modules in CAM and is still used as the NCAR default for climate simulations with 110 km grid spacings.

Additional details of the FV lat-lon dynamics package can be found in the tutorial 'The Lin-Rood Finite Volume (FV) Dynamical Core'.

The adaptive FV dynamical core has been run in two configurations: the full 3D hydrostatic dynamical core on the sphere and the corresponding 2D shallow water model that has been extracted out of the 3D version (Jablonowski 2004, Jablonowski et al. 2004, Jablonowski et al. 2006, St-Cyr et al. 2008, Jablonowski et al. 2009). In general, the shallow water system can be considered a 1-level version of the 3D dynamical core. This shallow water setup serves as an ideal testbed for the horizontal discretization and the 2D adaptive-mesh strategy. It further allows the efficient and quick testing of interpolation routines at fine-coarse grid interfaces.

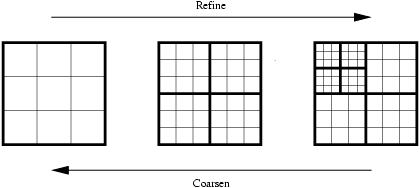
Both static and dynamic adaptation strategies have been tested. Static adaptations can be used to vary the resolution in pre-defined regions of interest. This includes static refinements near mountain ranges or static coarsenings in the longitudinal direction for the implementation of a so-called reduced grid in polar regions. Dynamic adaptations are based on flow characteristics and guided by refinement criteria that detect user-defined features of interest during a simulation. In particular, flow-based refinement criteria, such as vorticity or gradient indicators, have been tested. Refinements and coarsenings then occur according to pre-defined threshold values.

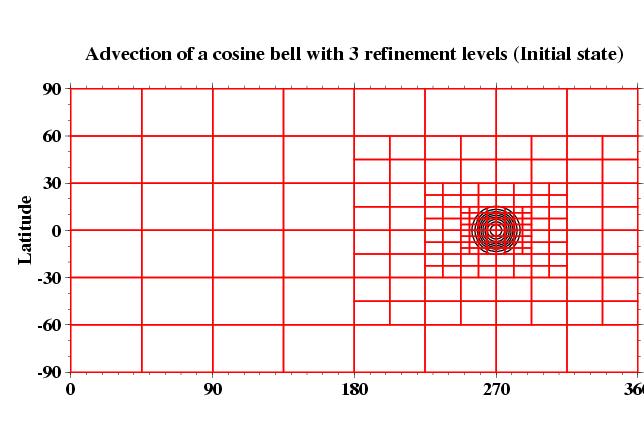
An example of an adaptive passive advection test on the sphere is shown below. The figure shows the initial conditions for the shallow water standard test case 1 with a 90^o rotation angle (see Williamson et a. 1992 for the test specifications). Here the adapted blocks track a cosine bell as it is transported once around the sphere. Note that each self-similar blocks contains 9x6 grid points in lon x lat direction so that the finest grid resolution in this example corresponds to a 0.625^o x 0.625^o grid. The maximum number of refinement levels is set to 3.



The adaptation criterion is based on a simple threshold assessment. A block is refined as soon as the height of the cosine bell exceeds a user-determined threshold value at (at least) one grid point within the block. On the other hand, a block gets coarsened if the height of the cosine bell in the block no longer meets the criterion. The corresponding mpeg movie (4.1 MB) shows that the cosine bell is successfully captured as indicated by the overlaid block distribution. The movie shows a 12-day simulation. After 12-days the tracer distribution returns to its initial position which then serves as the reference solution. There are no visible distortions of the height field as the cosine bell approaches, passes over and leaves the poles. The increased resolution clearly helps preserve the shape and peak amplitude. 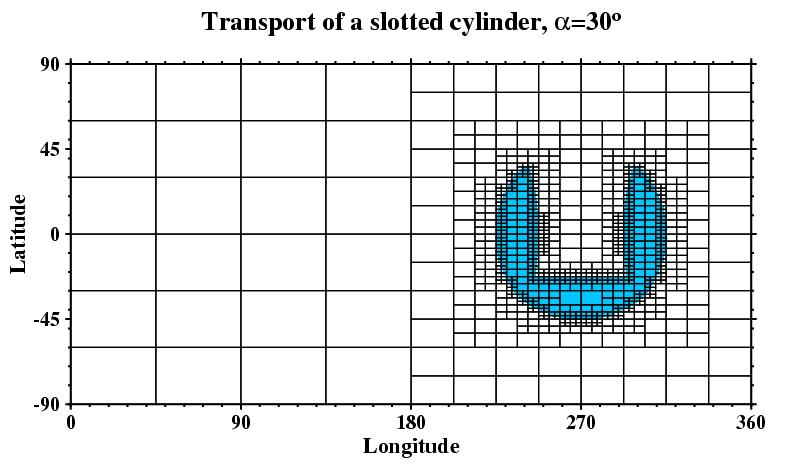The cosine bell represents a rather smooth tracer distribution. An alternative tracer field is shown below and also in this 12-day simulation (4.4 MB) with a rotation angle of 30^o. The slotted cylinder is initialized with a constant value and is set to zero outside the inner domain. The movie shows that the sharp edges are tracked successfully by a gradient-based refinement criterion.



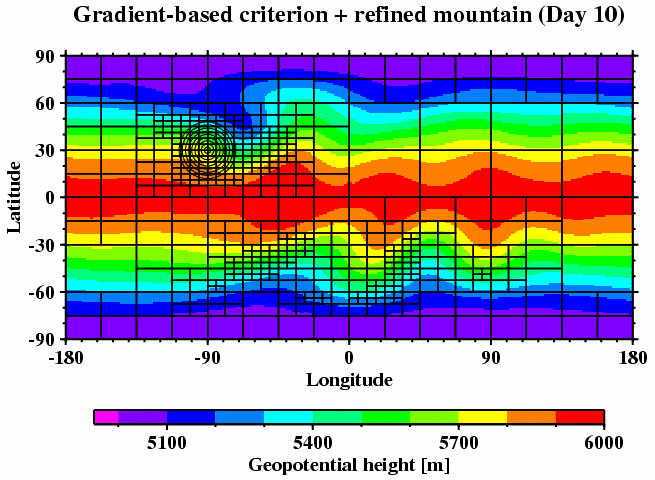
An example of a dynamically adapted nonlinear flow field is presented in the next figure. It shows an idealized flow over a single mountain at model day 10 (test case 5, Williamson et a. 1992). Here the adaptations are guided by the absolute value of the geopotential height gradient. The refined regions pick out the strong gradient regimes that are associated with the evolving wave train behind the mountain. Other refinement criteria are also feasible for this mountain-induced wave response. For example, the following 15-day mpeg movie (5 MB) shows the evolution of the geopotential height field that is dynamically tracked by a relative vorticity refinement criterion. It detects the evolving lee-side wave reliably and highlights slightly different refinement regions in comparison to the gradient criterion shown below.

The 3D adaptive finite-volume dynamical core on the latitude-longotude base grid has been assessed with a statically adaptive setup that utilizes prior knowledge of the developing flow field. The model is evaluated with the Jablonowski-Williamson baroclinic wave test case for dynamical cores of GCMs (Jablonowski and Williamson 2006). The flow field is characterized by a baroclinic wave train in the Northern Hemisphere that is triggered by a small perturbation superimposed upon the smooth initial zonal wind field.

The adapted blocks are used to refine the pre-determined storm track in the midlatitudes (Northern Hemisphere) with increasing horizontal resolutions. The refinements are confined to the horizontal directions so that the whole vertical column is refined in the event of refinement requests. Refinements are selected at the beginning of the forecast, which is followed by an analytical reinitialization step.

Here the analysis of the baroclinic wave train is focused on the surface pressure field. The two figures below show the surface pressure patterns for an adaptive model setup with (a) 1 and (b) 3 refinement levels at model day 8 (see also Jablonowski et al. (2009)). The adapted blocks are overlaid that illustrate the chosen band structure of the refinement approach. It can clearly be seen that the representation of the baroclinic wave improves significantly with an increasing number of refinement levels. The baroclinic wave intensifies as expected in the fine grid adaptive run and is rather damped on the coarser grid.

Carpenter, R. L., K. K. Droegemeier, P. R. Woodward and C. E. Hane, Application of the Piecewise Parabolic Method to Meteorological Modeling, Mon. Wea. Rev., 118, 586-612, 1990.

Colella, P. and P. R. Woodward, The Piecewise Parabolic Method (PPM) for Gas-Dynamical Simulations, J. Comput. Phys., 54, 174-201, 1984.

Ferguson, J. O., C. Jablonowski, H. Johansen, P. McCorquodale, P. Colella and P. A. Ullrich, Analyzing the Adaptive Mesh Refinement (AMR) characteristics of a high-order cubed-sphere 2D shallow water model, Mon. Wea. Rev., 144, 4641-4666, 2016

Ferguson, J. O., C. Jablonowski, and H. Johansen, Assessing Adaptive Mesh Refinement (AMR) in a Forced Shallow-Water Model with Moisture, Mon. Wea. Rev., Vol. 147, 3673–3692, 2019

Jablonowski, C., Adaptive Grids in Weather and Climate Modeling, Ph.D. dissertation, University of Michigan, Ann Arbor, MI, 2004 (download the pdf version, 8MB),

Jablonowski, C., M. Herzog, J. E. Penner, R. C. Oehmke, Q. F. Stout and B. van Leer, Adaptive Grids for Weather and Climate Models, ECMWF Seminar Proceedings on Recent Developments in Numerical Methods for Atmospheric and Ocean Modelling, Reading, UK, 6-10 September 2004, pp. 233-250 (download the pdf version 2MB)

Jablonowski, C., M. Herzog, J. E. Penner, R. C. Oehmke, Q. F. Stout, B. van Leer and K. G. Powell, Block-Structured Adaptive Grids on the Sphere: Advection Experiments, Mon. Wea. Rev., 134, 3691-3713, 2006

Jablonowski, C. and D. L. Williamson, A Baroclinic Instability Test Case for Atmospheric Model Dynamical Cores, Quarterly J. Roy. Met. Soc., 132, No. 621C, 2943-2975, 2006

Jablonowski, C., R. C. Oehmke and Q. F. Stout, Block-structured Adaptive Meshes and Reduced Grids for Atmospheric General Circulation Models, Phil. Transaction Royal Society A, 367, 4497-4522, 2009

Lin, S.-J., A Finite-Volume Integration Method for Computing the Pressure Forces in General Vertical Coordinates, Quart. J. Roy. Meteor. Soc., 123, 1749-1762, 1997.

Lin, S.-J., A "Vertically Lagrangian" Finite-Volume Dynamical Core for Global Models, Mon. Wea. Rev., 132, 2293-2307, 2004.

Lin, S.-J. and R. B. Rood, Multidimensional Flux-Form Semi-Lagrangian Scheme, Mon. Wea. Rev., 124, 2046-2070, 1996.

Lin, S.-J. and R. B. Rood, An Explicit Flux-Form Semi-Lagrangian Shallow Water Model on the Sphere, Quart. J. Roy. Meteor. Soc., 123, 2477-22498, 1997.

McCorquodale, P., P. A. Ullrich, H. Johansen, and P. Colella, An adaptive multiblock high-order finite-volume method for solving the shallow-water equations on the sphere. Communications in Applied Mathematics and Computational Science, 10 (2), 121–162, 2015.

Oehmke, R. C. and Q. F. Stout, Parallel Adaptive Blocks on a Sphere, in Proc. 11th SIAM Conference on Parallel Processing for Scientific Computing, 2001, CD-ROM.

Oehmke, R. C., High Performance Dynamic Array Structures, Ph.D. Dissertation, University of Michigan, Ann Arbor, 2004, Department of Electrical Engineering and Computer Science, 93 pp.

St-Cyr, A., C. Jablonowski, J. M. Dennis, H. M. Tufo and S. J. Thomas, A Comparison of Two Shallow Water Models with Non-Conforming Adaptive Grids, Mon. Wea. Rev., 136, 1898-1922, 2008.

van Leer, B., Towards the Ultimate Conservative Difference Scheme. II. Monotonicity and Conservation Combined in a Second-Order Scheme, J. Comput. Phys., 14, 361-370, 1974.

van Leer, B., Towards the Ultimate Conservative Difference Scheme. IV. A New Approach to Numerical Convection, J. Comput. Phys., 23, 276-299, 1977.

Williamson, D. L., J. B. Drake, J. J. Hack, R. Jakob and P. N. Swarztrauber, A Standard Test Set for Numerical Approximations to the Shallow Water Equations in Spherical Geometry, J. Comput. Phys., 102, 211-224, 1992