Practical "twang" instructions to set this Bach temperament by ear

Beats are important, yes; but the main principle here conceptually is interval quality. Please set the beat-counting aside for the moment! And forget the thinking in "cents" as that's a 19th century invention anyway. This page is about hearing amounts of spice in the sound.

7 July 2005, on the topic of "twang":

Since my harpsichord needed a fresh tonelift from today's rain anyway, I tried the whole thing with no beat-counting anywhere and did it only in terms of subjective "twang". No ratios, no logarithms, no other maths, no beat-matching of 3:2 or 1:1 or otherwise, but just pretending not to understand any of the maths and having a go, from experience with the sound. Worked out fine, and the details are below.

The explanation (unavoidably?) had some maths anyway but I'm trying to describe a process where the user doesn't need to understand them, if learning it in practice at a keyboard.... Only the feeling of single twang, double twang, and no twang. Qualities of the 4th or 5th, working with the tuning lever in hand.

 > Nobody in praxis
 > cared at Bach's time about the theoretical
 > concept of logarithms.

I agree with that observation, in the sense that musicians (whether then or now) really don't need to understand logarithms in any mathematical sense. What is important, however, is the concept of "sameness" whether it's in a drawing or on a keyboard or in a treatise.

Take, only for example, the common tuning of 1/4 syntonic comma meantone in its correct geometrical formulation. The eleven fifths are all geometrically the same size, whether this is expressed by a ratio or a logarithmic system or whatever. The diminished sixth "wolf" is whatever is left over where the circle does not close. The usable and correctly spelled triads all have exactly the same character as one another, because the fifths (which happen to be narrow) are all the same size, and the major thirds (happen to be pure 5:4) and minor thirds (somewhat narrow) are likewise the same as one another. The important thing is that sameness, which is geometrical and is NOT beat rates.

Basic knowledge to practical musicians of the 18th century (I believe), is how to set up whatever consistent variant of meantone suited their taste, whether those resulting major thirds are pure or a little bit wide or a little bit narrow...the correctly spelled major thirds are the same size as one another, as are the correctly spelled fifths that generate all 12 of the notes.

A basic harpsichord lesson in tuning is knowing how much twang belongs in a 5th, to deliver some overall quality when the whole layout is done. It's listening for interval quality whether one is codifying that with beat rates or not. After doing four 5ths in a row, test the resulting major 3rd against the starting note to see if it sounds pleasant, by whatever standard of expectation is in force. If not, start over by re- twanging those 5ths until we get something we enjoy. And at each 5th after that, test it against what we have already done (by a major 3rd) again to check pleasantness and sameness of quality. Keep going until all 12 notes are done, and we're done. Basic tasteful regularity, AKA "meantone" because the whole steps (e.g. C to D, and D to E) end up being exactly halfway (mean) within whatever major 3rd is in our taste. They have to be, because all 11 5ths are the same size in generating them. A whole tone is simply two of these regular 5ths, transposed back by an octave.

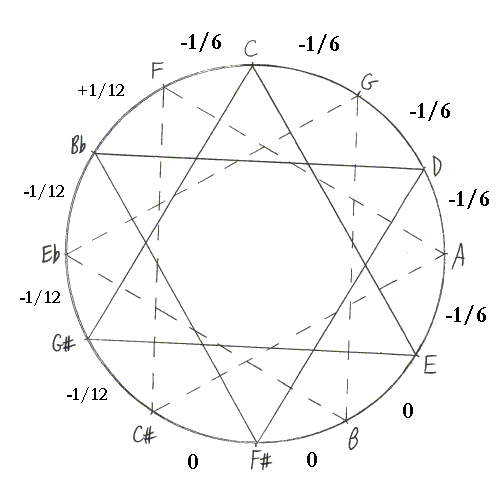
Now, move on to the Bach drawing where (as we agree at least for this) there are three of one single-looking thing, three of some other empty thing, and five of one doubly-looking thing. And a surd off one end or both, whatever's leftover after doing the main 11 by some scheme. Without use of any logarithms whatsoever, but rather thinking in ratios (so it's geometric rather than arithmetic), this could be taken as adjusting three of the fifths by ratio X, adjusting the next three as ratio Y, and the last five as ratio Z; and then whatever surd in the diminished 6th off the end.

• X ... X ... X.
• Y ... Y ... Y.
• Z ... Z ... Z ... Z ... Z.
• Leftover (surd, not directly calculated).

Let Y = 0 (i.e. pure 5th, no adjustment). Let X and Z be in some relationship where the adjustment of Z sounds to a musical ear like twice as much adjustment as X. Whether that's done by beat rates or just from experience listening for a certain amount of twang in the interval, there are three Xs the same as one another, and five Zs the same as one another, and Z has twice the twang adjustment of X.

Historically, the process of widening some of the 5ths away from their normal regular size (which here in this drawing is the five "Z" 5ths!) is called temperament ordinaire. It is a process using taste and experience. Some of the 5ths become less tempered (i.e. our "X" 5ths here), some might even become pure (our "Y" 5ths) or wide (our leftover diminished 6th), in that process of stretching some of the sharps higher and/or some of the flats lower, so they meet one another acceptably coming round the other side of the hill.

And Bach, not caring or even necessarily knowing about any numeric values in ratios or logarithms, has written down here a practical scheme to set up the twang in a way that works, having three different sizes of 5ths (one size being pure, and two tempered), plus whatever surd diminished 6th is hanging around.

One wouldn't even have to know that these bits of twang are called fractions of commas; but only how to do the thing, in sequence, in practice, working at an instrument. No numbers, no logarithms, no ratios. It's a way to adjust some common variant of regular (i.e. "meantone") layout, tastefully with temperament ordinaire principle giving some of the notes less twang than they would normally get in the cycle of setting all 11 5ths in sequence.

Hence my hypothesis. Straight across the 5ths (doing all the white notes first and then all the black notes, coming from the physical layout of a keyboard), F-C-G-D-A-E-B-F#-C#-G#-D#-A#. If there's something in the loop in the drawing, give it that amount of twang narrow in the setting of that 5th.

• F-C-G-D-A-E get double twang. Narrow each of these 5ths enough that we can hear it on medium-close listening. It's the same amount that one would do if setting the whole instrument in regular 1/6 comma; an amount learned by experience. That is, if we did all 11 of our 5ths by "double twang" we would end up with a complete regular 1/6 comma temperament, with its medium-sized wolf at the place where the ends don't meet.
• E-B-F#-C# get pure 5ths (no twang). They've been widened so much from normality that they've become pure.
• C#-G#-D#-A# get single twang. They're in between normal and pure, where the twanging is barely noticeable except on the closest listening.
• Leftover A#-F is a diminished 6th, it isn't tuned directly, and it simply needs not to be terrible. It ends up in this example being a single twang wide but that's only incidental.

It does not rely on any numerical crunching or anything electronic; it's just a practical method sitting at an instrument and doing the job, as (I believe) Bach would have done by taste and experience.

And having found something nicely workable, whether it's by himself or somebody who taught it to him, it's written down lest it ever get lost as a nice way to tweak a regular "meantone" into something more usable for more music.

Beat rates and other scientific measurement are just our modern way of getting it exactly the same from one occasion to the next, assigning numerical values (whether they're frequencies or beats or something logarithmic) to measure what has already been done intuitively and in practice.

The starting pitch to do this in practice can be taken from any convenient pitch source that plays a C, A, F, G, D, or E...since those are all on the line of the regular 5ths. Or for that matter, it's easy to take it from a B or an F# or a C# because those lead back by pure 5ths to E and we're into the regular line.

So (sitting in Bach's chair in front of a harpsichord) we can play any of these notes on whatever convenient instrument, like Jack Shepherd's oboe d'amore that he bought in Hamburg last week and has brought in to try with our harpsichord...play whatever note is most central to the other ensemble instrument, tune the harpsichord string to it, and then do the whole pattern outward in one or both directions where we stop at F going one way and stop at A# going the other way.

This is quite easy in practice, given that a specific tempering shape on that temperament ordinaire is in mind. (And here is my own practical sequence that I use regularly, setting the instrument accurately by ear in under 15 minutes.) The relationships of all these intervals stay the same, regardless of what starting frequency we're handed by the other instrument built by whatever nonstandard craftsman. The whole temperament moves up or down together, constant shape, whether we call this "Cammerton" or "Chorton" or "JackShepherdsOboeTon" or whatnot. We are not limited to any single starting frequency, the way all the beat-insisters are! The schemes of counting exactly one or two beats per second work only in a particular octave, and only with a forced starting frequency where everything will work out.

Sit down, do your 10 or 15 minute tuning at whatever the pitch du jour is, and play music. Inside such a thought-process, listening for the quality or spice of the 5ths, who cares about numbers? This is about musical listening, and practical experience tuning harpsichords at least a couple of times a week (putting ourselves into that 18th century milieu of a working musician not having time or inclination for mathematical calculation).

All the 16th-17th-18th century theorists who wrangled about various numerical systems are all well and good, for their own amusement and their own work. (Kirnberger too, added to that pantheon.) What would need to be demonstrated here--by any proponents of the counting of constant beats up the keyboard--is that Bach cared at all about any of that theory.

Sit down at the keyboard, put the right amounts of twang into the appropriate 5ths (by experience and by being taught), and play music. No mathematical computations required.

I personally don't care a whole lot about the math side of all that either, except that it's a convenient language with which to explain the musical results to mathematically-inclined people. My part in this has been to try to translate the language of that shape in Bach's drawing, to the more familiar language today of mathematical concepts (whether that's commas or logarithms or frequencies or beats)...it's all equivalency, and it's all merely measuring a concept that is not itself limited to mathematical constructs.

In summary: This whole temperament can be set up quickly and easily without counting any beat rates! One need only develop the skill to sense accurately where several 5ths/4ths have the same amount of tasty bite to them, and the experience to know how much of that is appropriate, and where it belongs. (This bite, technically, comes from the beats that give the interval an appropriate wobble: not at a constant rate to be counted, but a constant quality to be savored. The beats are there and that's what we are listening for, but not with numbers or clocks.)

This same twang thing is also especially useful when setting octaves carefully in the treble. Check each note for proper twanginess with the 4th and 5th below the top note, as it's being set. For example, checking the high octave G, if the C-G 5th and the D-G 4th don't have the same twang, the G is too high or too low to be a correct octave. And in testing an E it's supposed to twang against the A but be pure to the B.

Bradley Lehman

See also:

• [Instructions and explanation for beginning tuners-by-ear]
• [Expert instructions for advanced tuners-by-ear]
• Instructions for phone apps

Video demonstration on YouTube, August 2007: setting the Bach temperament

Video demonstration on YouTube, September 2007: setting late 17th century temperament ordinaire, and playing Purcell

Video demonstration on YouTube, August 2007: setting meantone accurately [Transcript of the captions]

Video demonstration on YouTube, August 2007: 1/6 comma meantone morphed into Bach

Return...