• Bach (Lehman, published 2005, which many call "Bach/Lehman 1722")
• Any regular temperament by ear
• Vallotti, Werckmeister, Neidhardt, Sorge, Young
• Lehman 2006 reading the Bach diagram in a different way
• Another Lehman temperament ordinaire, 2007 (more intensely colorful than the Bach)
• 17th century Germanic for Buxtehude, Froberger, Pachelbel, Kuhnau, et al, 2008
• Temperament ordinaire from Rameau's instructions and other clues, 2008
• Electronic device instructions for the Bach
• Instructions for phone apps

Bach

Recipe [Table]

• Get A from the tuning fork or other appropriate source.
• Tenor F-A (below middle C) beating wide 3 beats per second. It has 3 beats per second (or double the metronome speed of 89) if we are starting from A=440; or 2.8 beats (double the metronome 84) if starting from A=415. This establishes the boundary for the four intervening 5ths, F-C-G-D-A: our regular size of 5ths, 1/6 Pythagorean comma. All four of those 5ths will now become equally spaced within that region, tempered 1/6 comma each.
• Tenor F fourth down to C temporarily pure. (See why we're doing this temporary step...)
• Tenor A fifth down to D temporarily pure.
• Tenor G from that C and D so the fourth D-G beats 1.5 times as fast as the fifth C-G. (Triplets against duplets.)
• Middle C from the tenor F and that G, likewise: the fourth G-C beating as triplets against the duplets of the fifth F-C.
• Middle D from tenor G and A likewise.
• Correct the lower D and C to match these two.
• Middle E from tenor A slightly flat, same quality as these other fifths. It should beat as a major third from middle C at 4.5 times per second. (4.2 if you started from an A=415.) An excellent test for this particular F-A and C-E is found at bar 21 of the WTC book 1 C major prelude. These two major thirds should have exactly the same character as one another, although the beat rate is different (since the pitch is different). Coincidentally (?) this is at the golden mean of this piece.... The A-E fifth should beat exactly half as fast as our original F-A major 3rd, sharing the same A.
• Copy middle E down to tenor E. For especially careful accuracy, fuss with both these E's until all four of the following points are true:
  • (1) Whatever speed the tenor D-A 5th is, the fifth A-E across middle C should beat in 3/2 ratio from that speed (i.e. triplets vs duplets).
  • (2) Likewise, whatever speed the tenor F-A major 3rd is, the middle C-E major 3rd is triplets against its duplets. [We are up a fifth on the keyboard, and all frequencies are 3/2 as much.]
  • (3) Playing the tenor E as a 4th against tenor A, it should beat exactly half as fast as our original F-A major 3rd. Likewise, the A-E 5th we are testing across middle C should be exactly half as fast as our original F-A major 3rd.
  • (4) The octave E must of course be pure! Tune the intervening B pure with both of them.

• The above procedure has put all the naturals (except B) into regular 1/6 comma temperament, the same as the first half of "Vallotti": F-C-G-D-A-E all tempered identically. Bach's temperament finishes differently, as follows:
• Pure fifths E-B-F#-C#.
• Pure fifths F-Bb-Eb. This is a step to set the Eb exactly; we will move this temporary Bb soon.
• Tune G# pure to C# and then slightly lower it so the C#-G# fifth and the Ab-Eb fifth have the same quality: very slow beat from each.
• Lower Bb slightly so it has a slow beat from Eb like that of C#-G# and Ab-Eb.
• Play the first several bars of the C major fugue and the B major fugue, book 1, to check melodic and harmonic balances or to find any errors.
• Make all octaves and unisons pure to finish the instrument: all the bass, then all the treble.

This is coincidentally (?) an outstanding and perhaps ideal layout for all tonal music! It sounds like "equal" temperament in effect of its smoothness, but it has vivid color everywhere and is perceptibly different in every key.

See a mathematical analysis of the results, and the different version of the temperament for the Bach vocal music.

The complete explanation is in my Early Music article, February and May 2005.

Similarly, the tempering can begin from C or any other convenient note, instead of A. The important thing is to ensure that the geometric relationships of the results turn out correctly. It is just as easy to start the setup of this temperament from C as it is from A; the required result is simply that the naturals F-C-G-D-A-E all end up in regular 1/6 comma positions, relative to one another.

There is a PDF file for printout of the above instructions, as a better-formatted single page for handy reference. That is also one of the pages in the Oxford web supplement for part 2 of the article.

See also:

• [Instructions and explanation for beginning tuners-by-ear]
• ["Twang quality" instructions for intermediate tuners-by-ear]
• [The appropriate transposition for Bach's vocal music]
• [Video demonstrations]

Instructions for electronic tuners

Offset instructions for electronic devices are also at the front page.

Background: A process of adjustment, creating temperament ordinaire from a regular layout

These two three-page flowcharts are best studied by working through them step-by-step at a harpsichord, as I have done in 30 years of tuning by ear. They go through practical questions about the performance situation and the musical scores, and then through the listening and testing process for each note.

Bonus 1: setting up any regular temperament by ear

• Consider the notes in positions 1, 2, and 5 of a diatonic scale (for example: C, D, and G).
• When that fifth and that fourth are the same size, geometrically (i.e. having regular-size fifths generating the temperament), the beat rate of the fifth 1 to 5 is 2/3 as fast as the beat rate of the fourth 2 to 5. That is, it sounds like the rhythm of duplets against triplets, exactly.
• All one needs to know in setting up a regular temperament with any given size of fifth is the beat rate of one resulting major third: typically either the F-A below middle C, or the middle C-E. Everything else is derived from that single constant!
• Temporarily tune the fourth below the lower note pure to it, and the fifth below the upper note pure to it.
• Use these two to construct the note that is exactly midway between the notes of the original major third. In the example above, starting with F-A beating 3 times per second, we used the temporary C and D to construct a G that is exactly halfway (i.e. a "mean tone") between the F and A. Then we used F and G to construct the correct C above, and use G and A to construct the correct D above, always using that rule of duplets against triplets. F-C-G-D-A are now in regular positions.
• This same rule can be used to derive all twelve notes, working from duplets and triplets. It is always possible to visualize that 1-2-5 relationship, getting the third note from any two that are already correctly tuned. This is a good exercise for the reader....
• All the correctly spelled major thirds, in the regular temperaments, are the result of four equally-sized fifths. Therefore, all we are doing here (by analogy with origami) is folding by half and then by half again, to break our major third into four equal pieces. We can start with whatever size major third we want to, and the correct size of fifths is automatically generated by that "1, 2, and 5" procedure.

So, for example, to set up a regular 1/4 comma meantone layout, the generating major third of F-A is pure, zero beats. Drop a temporary C and D from those, construct the mean G, and go from there....

This same technique is explained again on the "tetrasecting" page, with a geometric diagram showing how and why it works. It is also described in more detail on the meantone page.

Bonus 2: some other refined temperaments contemporary with Bach's, for comparison

I derived each of these by looking at the resultant layouts (described by Lindley and others) and then coming up with a sequence that delivers those results easily, by ear. Other ways of getting to the same place may be possible.

And, it is easy to convert each of these to the others: by sticking to that common core of C-G-D-A in 1/6 comma 5ths. All these are "modified meantone", in that sense...starting from that core and then artfully combining other pure fifths and/or nicking steps, from F into the flat side, and from E into the sharp side, until they meet somewhere around the back. The process of sitting at an instrument and setting these up, in turn, is even more important as a learning experience than memorizing any of them!

"Equally tempered" in all these refers to quality, not equal beat rates. If we are tuning the middle note of a ninth, for example putting B equally tempered between E and F#, the upper 5th has to beat 1.5 times as fast as the lower one.

"VALLOTTI" (or misspelled as "Valotti" sometimes...)

The approximation most familiar today, with 1/6 Pythagorean comma: [Table]
Ab 0 Eb 0 Bb 0 F -120 C -120 G -120 D -120 A -120 E -120 B 0 F# 0 C# 0 G#

This simple 17th century Venetian temperament was known to Werckmeister in the 1680s, and resurfaced at various times later. It gets its name from mid-18th-century use by Vallotti and Tartini. It is extraordinarily easy to set up. It has become a de facto standard among many performers today.

As explained in part of my Early Music article, "Werckmeister III" is really a 1/6 comma temperament (!) disguised as a 1/4 Pyth comma temperament. It was Werckmeister's attempt to improve upon this particular Venetian scheme, and on the regular 1/6 comma meantone behind it. Werckmeister kept the C and the F# as fixed points and flattened some of the notes in between (i.e. by adding pipe material, not taking it away).

Vallotti:

• 1. F-C-G-D-A-E in regular 1/6 Pyth.
• 2. F-Bb-Eb-Ab-Db-Gb-Cb pure.
• 3. Check that the Cb makes a B such that the E-B fifth is 1/6 comma narrow like the other tempered fifths. If not, redo steps 1 and 2 more carefully until it is.

BARNES 1979? Tune all of VALLOTTI, but at the end tune the B pure from E instead of from Gb, and then check that it has made a decent residual 1/6 comma fifth with that F#. That is the only difference, the note B.

WERCKMEISTER III (1681/91)? Tune all of VALLOTTI first. Then bring C up to be pure with F. Put the G equally spaced (1/4 comma each) between this new C and the existing D. Nick A slightly flat by 1/12. Retune E pure from A, and B pure from E. End.

Note: this perspective on Werckmeister III doesn't preserve either the original A and/or C, and therefore this method probably should not be used with any ensemble music. But, it does show the relationship of structure between VALLOTTI and this, in sort of a crass way: tune a smooth VALLOTTI first and then make it lumpy by messing up five of the notes that had been in a regular pattern between fixed endpoints of F and B.... And, ponder what's happened to the F-A-C triad, melodically, by moving the A and C in opposite directions off their regular 1/6 (55-division) positions.

Werckmeister III is not a harpsichord temperament at all, and its musical effects are rough both melodically and harmonically. Rather, it is a money-saving organ conversion temperament from various regular (meantone) schemes, as I have explained in part 2 of the Early Music article.

YOUNG #1 1799/1800 [Theoretical version table] [Practical version table]

Easier practical version (1/6 Pythagorean comma):
Ab 0 Eb 0 Bb -60 F -60 C -120 G -120 D -120 A -120 E -60 B -60 F# 0 C# 0 G#

The practical difference is negligible (and inaudible) between these two versions. If they both have the same middle C, the G above it differs by only 0.03 Hz and the E by only 0.09 Hz. In cent values, the size of the C to G 5th is 697.92 vs 698.04; the size of the C to E major 3rd is 391.69 vs 392.18. (General principle: the basic sound of a temperament comes from its shape and relationships, not from super-precision of the number crunching. Which 5ths are tempered relative to which other 5ths? How are any pure 5ths and tempered 5ths put together in sequence? Which major or minor 3rds, if any, are pure or nearly so, or approaching their Pythagorean size?)

• 1. Tune all of VALLOTTI first.
• 2. Nick F downward slightly so it's equally tempered between C and Bb.
• 3. Nick B upward slightly so it's equally tempered between E and F#.

This temperament has suffered neglect both in its time and the 20th/21st centuries, because the mathematical formulation of 3/16 syntonic comma looks more complicated than it is in practice. Under the skin, though, it is this elegant VALLOTTI modification, with transition points of 1/12 comma 5ths between the regions of pure 5ths and 1/6 comma 5ths.

Yes, this temperament is from some 50 years after Bach's death, but it is here for practice in the procedure of modifying Vallotti! Notes are adjusted (I like the pun "tampered") to new average positions between a pure 5th and a neighboring tempered 5th. That is the way all these Neidhardt, Sorge, and Bach temperaments work also.

See Young's own formulation.... If Young was aware that his temperament is so close to Vallotti's (changing only two notes), he did not say so in that document. This similarity is obscured under his logarithmic calculations and monochord lengths.

YOUNG #2 1799/1800

• 1. Tune all of VALLOTTI first.
• 2. Retune F lower to be pure with C.
• 3. From F retune all of F-Bb-Eb-Ab-Db-Gb lower, as a cycle of pure 5ths. The B-Gb results as a tempered 5th like those of A-E-B near it.

• 1. Start from a C fork.
• 2. Tune the major 3rd E above middle C to be between 4 and 4.5 beats per second.
• 3. Tune all of C-F-Bb-Eb-Ab-Db-Gb pure as 5ths.
• 4. Place the B so it is average in character against both the E and the Gb.
• 5. Use this same character into each of the 5ths C-G-D-A-E, without moving either C or E.
• 6. For greater precision in this, set the D using a temporarily pure C-G 5th and A-E 5th below middle C. This is to place the D exactly midway within C-E. Then correct G to be average character against both C and D; correct A likewise against D and E.

The Young #2 table is at page 19 in the PDF supplements ("44 full-page analyses"); see the outline page to download it.

NEIDHARDT 1724 "Village", 1732 "Small City" [Table]

• 1. C-G-D-A-E-B in regular 1/6 Pyth.
• 2. C-F-Bb pure.
• 3. B-F#-C#-G# pure.
• 4. Eb equally tempered from G# and Bb.
• 5. Nick B up so it's equally tempered between E and F#.
• Note: this version is correct here, as of 8/31/05. [Details]

NEIDHARDT 1724 "Small City", 1732 "Big City"

• 1. F-C-G-D-A-E in regular 1/6 Pyth.
• 2. F-Bb-Eb-Ab pure.
• 3. E-B-F# pure.
• 4. C# equally tempered from F# and G#.
• 5. Nick E upward so it's equally tempered between A and B.
• 6. Retune B pure from the new E.
• 7. Nick F downward so it's equally tempered between Bb and C.

NEIDHARDT 1724 "Big City" [Table]

• 1. Do all the steps 1-6 of Small City.
• 2. Retune F down so it's now pure from C.
• 3. Nick Bb downward so it's equally tempered between F and Eb.
• Note: this version is correct here, as of 11/05/05. [Details]

NEIDHARDT 1732 "Third-Circle #4" [Table]

• 1. F-C-G-D-A-E in regular 1/6 Pyth.
• 2. F-Bb-Eb-Ab pure.
• 3. E-B-F# pure.
• 4. C# equally tempered from F# and G#.
• 5. Retune F down so it's now pure from C.
• 6. Retune E up so it's now pure from A.
• 7. Nick D# downward the slightest bit (1/12) which improves it with B, and makes it slightly wide from Bb.

Concerning this "Third-Circle #4" temperament, there is an interesting draft article by Margo Schulter posted to rec.music.early on 8 March 2005, soon after reading the first half (only) of my Early Music article. Among generally excellent comments there lurks a minor problem: she (and at least one other writer I've seen who also relies on Barbour's book as main source) has made the incorrect assumption from Barbour's footnotes that Neidhardt presented this temperament in 1724. It made its first appearance in 1732, as can be seen by comparing the 1724 and 1732 documents.

These Neidhardt layouts from 1724 and 1732 do fairly well in Bach, except for pieces such as the Bb minor, F minor, and G minor preludes of WTC 1, and similarly some of the organ music in F minor, C minor, G minor, and E-flat major. The rawness of Ab-C stands out rather suddenly within musical contexts of tonal motion (and admittedly, this is a subtle point). Listen especially to the exposed Ab-C and Db-F in bars 14-15 of the Bb minor prelude, WTC 1.

The most basic technical cause of that problem is the assumption that G# should be relatively closer to the central C major tonality than Ab: leading to an interval E-G# that is smaller than Ab-C. I have explained this problem in the Clavichord International article and here at the "ordinary" page. I believe that all temperaments having E-G# smaller than Ab-C are doomed to sound suddenly rough, in such passages in Bach's music, for that same reason.

From this "Third-Circle #4" if one lowers the Bb a bit (by one or two 1/12ths to taste), thereby softening F#-A# and getting rid of the wide Eb-Bb 5th, the resulting temperament is especially smooth: try it. But, in my opinion, it still has the flaw of an Ab-C that is slightly too wide for the musical contexts it sets up, especially in an exposed-10th spacing. I have played through all of WTC book 1 in such a modified version of this Neidhardt temperament (John O'Donnell's proposed "Bach" temperament), and I feel it works very well overall...but in such a straight-through and long session, it is a bit too bland, too ordinary. I do not feel that it inspires my phrasing, as a player, as much as I sense from my favored layout.

SORGE 1744 "Good for Cammerton harpsichords" [Table]

• 1. F-C-G-D-A-E in regular 1/6 Pyth.
• 2. F-Bb-Eb-Ab-Db pure.
• 3. Retune F down so it's now pure from C.
• 4. Nick Bb downward so it's equally tempered between F and Eb.
• 5. Tune B pure from E.
• 6. Put F# so it's equally tempered between B and C#.
• 7. Nick E upward so it becomes pure from A.

SORGE 1758 "Good for Chorton organs" [Table]

This is the closest "relative" I have yet found for Bach's temperament, among documented keyboard temperaments. I believe it likely that Sorge copied Bach's method from the Leipzig organs at some time during the 1740s or 50s and then reformulated it as this. In the result, eight of the notes are identical to Bach's. The other four notes have logical adjustments that show this to be a hybrid between equal temperament and Bach's. (Details are in my Early Music article....)

• 1. F-C-G-D-A-E in regular 1/6 Pyth.
• 2. E-B-F#-C# pure.
• 3. F-Bb-Eb pure.
• 4. Put G# equally tempered between C# and D#.
• 5. Nick E upward so it's equally tempered between A and B.
• 6. Retune B pure to this new E.
• 7. Retune F down so it's now pure from C.
• 8. Nick Bb downward so it's equally tempered between F and Eb.
• 9. Nick C# downward so it's now pure from G#.

BACH 1722 (repeated) [Table]

• 1. F-C-G-D-A-E in regular 1/6 Pyth.
• 2. E-B-F#-C# pure.
• 3. F-Bb-Eb pure.
• 4. Put G# equally tempered between C# and D#.
• 5. Nick Bb downward so the Eb-Bb fifth has the slightest wobble, like the C#-G# fifth. Bb-F will have that same wobble, but wide rather than narrow.

These temperaments, among others, appear at this summary comparison page.

Bonus 3: an easy Lehman temperament: using musical listening skills for quality, not mathematical beat-counting

I have formulated this temperament also from elements in the Bach drawing, but in a less obvious way. (Full discussion of it is in my review of O'Donnell's article.) I still like my first one better, overall, while this one works very well in the same repertoire. Both are equally easy to set up in practice.

• C from fork, and over to middle C.
• Set E from C, somewhere near the quality of regular 1/6 comma (i.e. with the familiar sound from Vallotti, or slightly sharper than in Werckmeister 3). If it happens to be a little high or low to taste, that's OK. We just want to stay out of the range where it's so high that C-E turn into a blur, or so low that there's no room left to work with in the following steps.
• Fit the G, D, and A into this so C-G-D-A-E all have the same quality as 5ths or 4ths. Whatever regular size we're setting here, this is our basic unit.
• From E, pure B, pure F#. G-B should sound slightly "harder" or brighter than C-E, and then D-F# even more so.
• From C, pure F. F-A has the same character as G-B. The C major, F major, and G major triads are our three best.
• From F, temper Bb as a narrow 5th (or wide 4th) of approximately the same quality as the others above. Listen also that Bb-D is similar quality to the F-A already available; and that F#-A# is high but acceptable-sounding.
• From Bb, pure Eb. Confirm that Eb-G and D-F# have the same quality as one another, both sounding much like they do in equal temperament. Confirm also that B-D# has approximately the same character as F#-A#, and the whole triad B-D#-F# is quite good, owing in part to the pure 5th.
• From Eb, make Ab a narrow 5th or wide 4th of approximately the same quality again, or perhaps a little bit gentler to taste. Test that E-G# is high and bright, but not quite as wide as Pythagorean. Ab-C should sound very slightly wider in character than Eb-G does, but still a good complete triad Ab-C-Eb.
• From F#, make C# a narrow 5th or wide 4th similarly. Check that A-C# makes a nice transitional character between D-F# and E-G#. Also check that Db-F has a character resembling that of B-D#. Finally, note that our leftover interval C# to G# is probably slightly wide as a 5th (or narrow as a 4th), but that the character of C#-G# sounds the same as Eb-G#. They simply happen to be tempered in opposite directions, but a similar amount, not that anyone would notice during the playing of music.

Play suitable music in a variety of keys, to test that everything works nicely.

Bonus 4: yet another Lehman circulating temperament based on listening for quality (27 October 2007)

• Get A from a tuning fork, and make a pure octave down to tenor A.
• Tune F as a major 3rd below tenor A, and make it 2 to 3 beats wide: moderately tempered, and with a gentle vibrato. (Try it differently on different occasions, to work out what serves best on this particular instrument in this acoustical space.) This will give us anything from about 1/5 comma to 1/6 on the naturals, automatically generated by the following set of instructions. If you pick 3 beats per second you get 1/6 comma.
• Build two temporary notes: tenor C below tenor F pure as a 4th, and tenor D below tenor A pure as a 5th. These are being done only so we can put the G exactly where it belongs between F and A, using these two reference points.
• Working from that C up to tenor G as a 5th, and from that D up to tenor G as a 4th, put G where it has exactly the same quality from both. It will be fairly rough from both. The 4th will be beating faster than the 5th, and if you care to count beats, you have reached the correct point when the 4th is beating as triplets against the 5th as duplets.
• Working from that tenor G and tenor A up to the D above middle C, similarly put the D into position so the G-D 5th and the A-D 4th have the same quality as one another. Again the 4th will be beating as triplets against the duplets of the 5th. This is always true when doing correctly equalized 5ths/4ths, playing the notes that are under the fingers 5-4-1 of the left hand.
• From this middle D, correct the lower temporary D to be a pure octave. Check it with both G and A for equal roughness.
• Working from tenor F and tenor G up to middle C, put C into place so the F-C 5th and G-C 4th are equally rough. Same triplets-against-duplets shtick.
• From middle C fix the lower C as pure octave, and check its 4th and 5th.
• Now F-C-G-D-A are all similarly tempered with one another, smoothly. Regular meantone!
• Copy tenor F up to middle F as a pure octave.
• From tenor A, tune middle C# as high as you can bear it, testing also as the Db to F major 3rd above it. I usually try to get these two as equal in quality as I can. Some others might prefer to put C# a bit lower, favoring it as A-C# instead of Db-F.
• From tenor A build a temporary pure E 4th under it. From that C# build a temporary tenor F# pure as a 5th. We are going to use both of these to build a correct B next to middle C.
• Make a B that is equally rough from both that E as a 5th, and F# as a 4th. As usual, the 4th makes triplets against the 5th's duplets.
• From B and C# build the F# above middle C. Both these intervals will be pure or nearly so. Copy it down to tenor F# erasing the temporary one we did a moment ago.
• From A and B build the E above middle C. Put most or all of the tempering into A-E, and little or none into B-E. Check E also with middle C; we don't want it to be worse in quality than our starting F-A was. It will be beating faster than F-A, merely because the notes are higher in pitch, but the quality should be the same...and B-E will work out to be pure or nearly so.
• Copy it down to tenor E erasing the temporary one.
• We're almost done. We already have F-C-G-D-A-E-B-F#-C#. We only lack G#, Bb, and Eb.
• Copy middle C# down to tenor C# as a pure octave.
• Build G# from C# as a 5th, either pure or slightly narrow. Check it as a major 3rd above E also, that it is plenty high...and that this resembles the A-C# major 3rd's quality.
• Tune Bb as a 5th under F, either pure or slightly wide (which will improve it as a major 3rd in F#-A#, without much cost to Bb-D).
• Working from G# and Bb put middle Eb where it sounds best.
• Copy middle Eb down to tenor Eb.
• Play through all twelve major triads listening for usability of all of them, but also an interesting variety. The sharp keys should be bright and penetrating, and the flat keys comparatively mellow. F major, C major, and G major should be calmest.
• Go back to C# and check it one more time, maybe nudging it slightly, until you like both A major and Db major as much as you want to.
• Finish the instrument by octaves.
• Play through something suitably intense and expressionistic to test the instrument. The slow movements in B minor and C minor by Wilhelm Friedemann Bach, pages 20 and 32 in the Henle edition #452, do very nicely with all the cross-relations and such.

Bonus 5: Lehman ordinary temperament for Buxtehude, Reincken, Froberger, Kuhnau, Böhm, et al (20 June 2008)

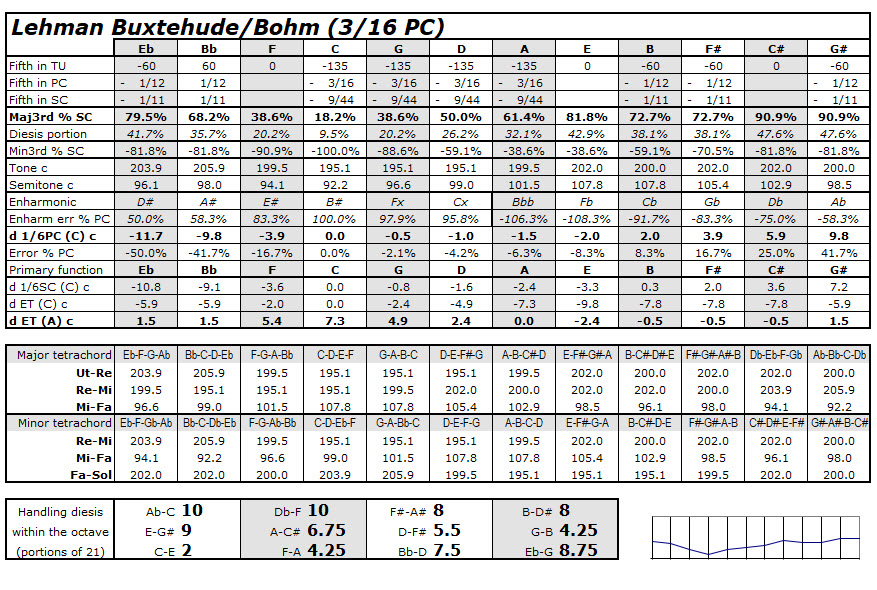
The tempering in C-G-D-A-E is 3/16 Pythagorean comma, which is (for all practical purposes) the same as 1/5 syntonic comma. Starting from regular 1/5 syntonic comma, it is very easy to set the remaining notes by ear.

It comes from analysis of the actual keys, scales, and notes used by these composers, plus temperament ordinaire principles of sharpening sharps and flattening flats. Smoothness and resonance are emphasized in the keys most often used as tonics: C, F, G, D, A, and B-flat majors, and D, A, G, E, C, B, F, F# minors.

At the same time, individual notes are all carefully placed harmonically and melodically, so they can be used as needed within these compositions: F#, C#, G#, D#, A#, E#, B#, Bb, Eb, Ab, Db, Gb, Cb. The occasional triads such as B major, F# major, Ab major, and C# major are spicy with high 3rds, but nowhere near as raucous as their counterparts in regular meantone layouts (where some of those notes are normally misspelled). These triads are also gentler and smoother than they are in Werckmeister III.

Major 3rds better than (smaller than) their counterparts in equal temperament: C-E, G-B, F-A, D-F#, A-C#. For music in the major and minor scales, and in the various church modes, those are the major 3rds most frequently needed to be consonant.

Major 3rds slightly wider than in equal temperament: Bb-D, B-D#, F#-A#, Eb-G, E-G#, Ab-C, Db-F. This spiciness is an expressive asset whenever diminished 4ths occur in the music...and that is a remarkably frequent occurrence in this repertoire: C#-F (often within D minor), G#-C (in A minor), A#-D (in B minor), B-Eb (in C minor), F#-Bb (in G minor), D#-G (in E minor), E-Ab (in F minor).

My postings about this on HPSCHD-L, including rosters of music by Buxtehude and Böhm analyzed for the notes needed:

[Going through the music to see what notes it needs (6/20/08), and then presenting a 1/5 comma ordinaire temperament]
[Some videos illustrating that tempering style (6/23)]
[Some remarks why it's important, noting how similar the style of the music is from Reincken forward (6/23)]
[Why I switched away from a 1/4 comma base to 1/5 and 1/6 (6/24)]
[Summary of tempering strategies (6/24)]
[Presenting the reasoning process, as a summary (6/26)]

Try the following sequence:

• Get C from a tuning fork. Copy to middle C.
• Set E as a major 3rd above middle C beating about 3 times per second, raised above the point where the interval would be pure. (This is the same as it does in Werckmeister III, or in 1/5 syntonic comma meantone. Regular 1/5 was popular in the 17th century; see Mark Lindley's article "Temperaments" in New Grove.)
• Build two temporary notes: tenor G below middle C pure as a 4th, and tenor A below middle E pure as a 5th. These are being done only so we can put the D exactly where it belongs between C and E, using these two reference points.
• Working from that G up to middle D as a 5th, and from that A up to middle D as a 4th, put D where it has exactly the same quality from both. It will be fairly rough from both, but we will fix this in the next two steps. The 4th will be beating faster than the 5th, and if you care to count beats, you have reached the correct point when the 4th is beating as triplets against the 5th as duplets.
• Move the temporary G down slightly until the G-C 4th and G-D 5th have the same average quality as one another.
• Move the temporary A up slightly until the D-A 4th and A-E 5th have the same average quality as one another.
• Check C-G-D-A-E to be sure all these 4ths or 5ths have similar tempering.
• Tune F pure from C.
• Tune B pure from E.
• Tune Bb pure from F, and then Eb pure from Bb.
• Tune F# pure as a 5th from B, and then nudge it slightly flat so it barely begins to beat.
• Tune C# pure from F#, and nudge it slightly flat until it barely begins to beat.
• Tune G# pure from C#, and check that it is beating slightly with Eb.
• Go back to Bb and nudge it downward slightly, so the 5th from Bb-F begins to beat very slowly, wide.
• Finish the instrument by octaves.
• Play through mid-to-late 17th century German repertoire: Buxtehude, Pachelbel, Böhm, Kuhnau, et al, and some Francois Couperin (E major, A major, C minor, F minor, ...).

Or, this simple sequence starting from a tuning app that offers regular 1/5 syntonic comma:

• From a tuning app calibrated to regular 1/5 syntonic comma, tune C, G, D, A, and E.
• Check C-G-D-A-E to be sure all these 4ths or 5ths have similar tempering.
• Tune F pure from C.
• Tune B pure from E.
• Tune Bb pure from F, and then Eb pure from Bb.
• Tune F# pure as a 5th from B, and then nudge it slightly flat so it barely begins to beat.
• Tune C# pure from F#, and nudge it slightly flat until it barely begins to beat.
• Tune G# pure from C#, and check that it is beating slightly with Eb.
• Go back to Bb and nudge it downward slightly, so the 5th from Bb-F begins to beat very slowly, wide.
• Finish the instrument by octaves.

Or, set all of it from an app that allows custom temperaments, using cent offsets from equal temperament. Those values are shown here in the table, using the line "d ET (C) c" (the offsets when holding C at its place from equal temperament), or the line "d ET (A) c" (the offsets when using A from equal temperament). Arranged chromatically and using the line for A, that is:

• C +7.3
• C# -0.5
• D +2.4
• Eb +1.5
• E -2.4
• F +5.4
• F# -0.5
• G +4.9
• G# +1.5
• A 0.0
• Bb +1.5
• B -0.5

Demonstrations of this temperament: [Part 1] [Part 2]

Bonus 6: Interpretations of Rameau's 1726 temperaments: C version in 1/4 syntonic comma, and his preferred Bb version in 1/6 (19 November 2008)

(Preliminary presentation; further details being worked out for a more substantial article about this.)

In Jean-Philippe Rameau's Nouveau systeme de Musique (1726), chapter 24, [Transcription] he described several temperaments that are modifications of regular meantone. One of them has the series of regularly-tempered intervals starting on C, and the other includes F and Bb as well. He preferred the latter layout, as it "conserve toute la justesse possible dans les modulations les plus usitees" (keeps the best purity in the most-used keys; bottom of page 110). He brought up this Bb temperament as a contrast against the 1/4 comma C temperament he had just described.

Rameau later (1737) changed his preference to equal temperament.

Rameau's 1726 presentation of a C-based temperament is clearly about the use of 1/4 syntonic comma division. His section about his preferred Bb-based temperament, however, appears to be about the use of 1/6 comma division instead of 1/4. It begins at the bottom of page 110; I have been studying it from two facsimile editions: one edited by Kremer (Zurfluh 1996), and the other by Jacobi (American Institute of Musicology 1967). He says that this temperament unites the differences between the two commas, i.e. the syntonic and the Pythagorean, into a single solution. It is a practical and musical solution, not a theoretical/mathematical abstraction that fits neatly into the exact marks hit by overtones.

Furthermore, simple experimentation reveals that a 1/4 comma division starting on Bb does not work well in practice; it has to be a gentler division such as 1/6 for the notes around A# (D#, E#, and B#) to sound sufficiently smooth in Rameau's music.

That harpsichord music is:

• Premier livre (1706)
• Pieces de Clavecin (1724, reprinted 1731)
• Nouvelles Suites de Pieces de Clavecin (c1728-9)
• Pieces de Clavecin en Concerts (1741, ensemble, including five rearranged as harpsichord solos)
• La Dauphine (manuscript 1747)

Rameau's published harpsichord music before 1737 uses these notes: Db, Ab, Eb, Bb, F, C, G, D, A, E, B, F#, C#, G#, D#, A#, E#, and B#. Because individual pieces go beyond 12 notes, and especially if we assume the harpsichord is not to be retuned during a suite, we must seek solutions that have good compromises for all these notes. We need good-sounding D#, A#, E#, B# in all their contexts without too much damage to Eb, Bb, F, C; we need placements of Db/C# and Ab/G# that work well as either note.

The harpsichord parts in the 1741 book similarly use all those notes from Db up to E# (no B#). In the second Menuet of the second concert, the chromatic phrases at bars 6-7 and 18-19 include enharmonic shifts from C# to Db. La Dauphine of 1747 requires all the notes from Ab to G#; see especially the enharmonic shift from G# in bar 35 to Ab in bar 36. That Ab in the bass (replacing the G#) is the only note that changes within those otherwise identically repeated phrases. It makes the music shift immediately from the D minor of the preceding bars (and a decorated A major dominant) into C minor.

In the 1/6 comma layouts, having put all of Bb-F-C-G-D-A-E-B-F# into position first, I placed the Ab/G# so the major 3rds Ab-C and E-G# are both the same size. Finally, I placed the C# and Eb into easy-to-find positions within F#-C#-G# and Ab-Eb-Bb, testing various triads and passages from Rameau's music. I present here several possibilities, all proceeding from a regular cycle of Bb-F-C-G-D-A-E-B. I worked these out at the harpsichord, only later transferring them into my spreadsheets for this report. The first four all sound good to me, especially the one with the lowered D#, and they are easy to do quickly by ear.

The fifth one alerted me that the history books are mistaken, with regard to Rameau's 1726 preference being a 1/4 syntonic comma layout beginning on Bb. It does not work, in Rameau's own published harpsichord music of the 1720s! The A#, D#, and E# are too high, given that the music uses them so frequently and in such direct harmonies as B major, F# major, and C# major triads. There is similarly a problem in Rameau's G minor and G major music of the 1720s, wherever there is a trilled Bb-A over D and F#. The premise of regular 1/4 comma from Bb-F-C-G-D-A-E-B leads inevitably to absurd musical conclusions in Rameau's music; therefore, the premise itself is wrong and must be discarded.

20th century writers (Barbour, Lindley, Devie, Jorgensen...) missed this switch away from 1/4 comma, apparently because they have assumed that Rameau's introductory phrase ("Pour que les Intervales conservent toute la justesse possible dans les Modulations les plus usitées...") on p110 takes "justesse" as referring to pure major 3rds. However, Rameau was clearly referring to purity of playability and regularity through all the most commonly used harmonies, not the short-sighted goal of beatless major 3rds. [The relevant sections: Barbour p135; Lindley Stimmung und Temperatur pp232-247; Devie pp95-105; Jorgensen Tuning pp189-213; Lindley New Grove pp252-3 and 256-7.] Lindley's New Grove article does not bother to mention that Rameau had two different temperaments in the 1726 book, although Lindley had presented hypothetical layouts of both on page 235 of Stimmung und Temperatur. Devie's three tables (figures 32-34 on p98) are all 1/4 comma layouts based on Gallimard (1754), a math book rather than a music book, instead of deriving them directly from Rameau's publication.

To test these temperaments in action, I played through all of Rameau's harpsichord music, and Francois Couperin's fourth book (published 1730, but it says he had completed all the music by 1727). Couperin's Ordres 21 and 23-27 in that fourth book make especially wide demands on a temperament. I played also the D major and C minor suites by Antoine Forqueray, since it makes similar demands of the notes D#, A#, Ab, Db, and extends as far as Gb (within the same C minor music that needs C# and F#). [Forqueray (c1671-1745). This music was published in 1747 by Forqueray's son, both as compositions for viola da gamba and as harpsichord-solo arrangements. Obviously, they had some suitable harpsichord temperament that handled all these notes well: to play not only the harpsichord version, but also for accompaniment in the ensemble version.]

In all this music, particularly with the way it gets into the highest sharps (D#, A#, E#, B#) while also needing Ab and Db, anything tighter than a 1/6 comma base sounds too harsh to me, ruining the gracefulness of the music.

• 1 based on Bb: Bb-F-C-G-D-A-E-B 1/6 Pythagorean comma; B-F# 1/12; F#-C# pure; Ab/G# equalized within E-x-C as major 3rds; Eb tempered the same from both Ab below and Bb above. Result: the three wide 5ths are C#-G#-D#-A#, each only by a scarcely noticeable 1/12 comma. [Table] Four of the major 3rds have size 3. Db-F and B-D# are 12, and F#-A# is 14.
• 2 based on Bb (and lowering the D#): Same as above, but lowering the note D# by an additional 1/12, so the B-D# sounds better. Ab-Eb becomes pure, and Eb-Bb becomes 1/6 comma wide instead of 1/12. B-D# becomes the same size as in Pythagorean, rather than slightly wider than that. [Table] Four of the major 3rds have size 3. Db-F is 12, F#-A# is 14, and B-D# is 11.
• 3 based on Bb: Bb-F-C-G-D-A-E-B 1/6 syntonic comma; B-F#-C# each 1/12 comma; Ab/G# equalized within E-x-C as major 3rds; D# pure from G#; the two wide 5ths C#-G# and Eb-Bb are both the same size as each other. The crucial note to get right, tastefully, is the D#: beating slightly wide under the Bb. Then, tune the G# pure under D#, and check that it is only slightly wide from C#. [Table] Four of the major 3rds have size 3.7. Db-F is 11.8, F#-A# is 12.8, and B-D# is 10.5.
• 4 based on C: C-G-D-A-E-B-F#-C# 1/4 syntonic comma; C#-G# pure; C-F pure; Bb and Eb each made progressively wide as 5ths descending from F. [Table] Four of the major 3rds (C-E, G-B, D-F#, A-C#) have size 0. Eb-G is 12.5, F#-A# is 13.75, and Ab-C and Db-F are each 18.25. The notes D# and A# work well, at some expense to Eb and Bb.
• 5 (not as good) based on Bb: Bb-F-C-G-D-A-E-B 1/4 syntonic comma; B-F#-C#-G# each pure; Eb fit into an intermediate position, slightly better with Bb than with G#. [Table] Four of the major 3rds (Bb-D, F-A, C-E, and G-B) have size 0. Ab-C is 12.75, B-D# is 15, Db-F is 15.5, and F#-A# is 18.25. The A# seems to me to be too high for the music, occurring so frequently within the common keys of D major and E minor. D# is similarly too high for music in A minor or E minor.

My own preference as a practicing harpsichordist is for the 1/6 comma solutions 2 and (especially) 3: both treating the important note D# kindly, especially because so much of Rameau's harpsichord music of the 1720s is in A minor, A major, E minor, and E major. The sonority of D-F#-Bb (or D-F#-A#) also occurs frequently in the 1728 book, within the G minor and G major music.

Further evidence (admittedly circumstantial) away from 1/4 comma is in the "Remarques sur les Pieces de ce Livre, & sur les differens genres de Musique" of Rameau's c1728-9 volume of harpsichord music. [Scans from Bärenreiter 3800, 1972, ed. Erwin Jacobi: page 1, page 2; print it at a reduction to approximately 50%] Rameau devoted seven paragraphs to the theoretical explanation of enharmonic shifts. He called special attention to "L'enharmonique", and to a spot in "La Triomphante" that has B# in the left hand and C natural in the right hand at the same time. He carefully described the theoretical "difference of one Quarter-tone" between such pairs, theoretically, but emphasized that they are exactly the same key on the keyboard. He also explained the theoretical difference between Diatonic and Chromatic semitones.

Most importantly, in this section, his point was that the oddities come from musical usage by the composer: not from the physical properties of a strongly nuanced keyboard temperament. In his view, apparently, it does not come from a situation where one note of an enharmonic pair is in tune on the keyboard while the other is grossly out of tune (by as much as a "Quarter tone"), which is given by a 1/4 comma basis (where C# and Db are a diesis apart, about 42 cents). If this enharmonic shifting were directly perceptible, immediately, within his style of tuning (using the conjecture of 1/4 comma, and with sharps and flats compromised somewhere within a diesis span of difference), I believe he would have said so here. He would have explained why the G# in bars 15-16 and the Ab in bar 17 of "L'enharmonique" (or the C# in 52-3 vs the Db in 54) do not both sound reasonably in tune, simultaneously. He at least would have said something about getting the C# up high enough (obviously impure enough from A) to sound reasonable as a Db under the treble F.

Therefore, I must conclude that by 1728-9 he wasn't promoting as first preference a temperament as extreme as 1/4 comma among the naturals and Bb. It had to be more moderate than that, toward equal: at least as lightly tempered as 1/6 comma in the naturals and Bb, and with all the other sharps and flats at compromised/intermediate positions for their contexts, such that the enharmonic shifts in the music were not obvious. In the way he described his compositional theory here, the startling nature of enharmonic shifts came not from the physical phenomenon of one note (or the other) being far out of tune, but rather from subtle and clever features of the composition.

Coming to this from hands-on tuning practice, which makes the point most directly (in sound instead of on paper, or a computer screen): if it were based on 1/4 comma instead of 1/6, all for the questionable goal of getting the major 3rds Bb-D, F-A, C-E, and G-B all to be as small as pure 5:4 (or G-B slightly wider by raising the B), the losses elsewhere have to be greater. If we base it on 1/4, the notes D#, A#, E#, and B# are all garishly high, and the Ab and Db (and Gb) are disturbingly low. Did Rameau really want such an extreme approach, before changing his mind and going with equal? Or, was he writing about a more moderate middle ground?

Restating that practical point: if the Bb-F-C-G-D-A-E are all established first in regular 1/4 syntonic comma, it is not possible to fit the remaining notes into any places such that all of C#, G#, D#, A#, Eb, Ab, and Db will sound reasonable...let alone E# and B#. Try it. Among other problems in the vicinity, F# cannot be pulled up high enough to make F#-A# in any way consonant; even if B is raised aggressively from E, and B-F# is made as much as 1/3 comma wide (going against Rameau's instructions to make B-F# "less tempered"), it still does not work. F# does not get high enough to make a decent major 3rd under the given A#. Set up a temperament with regular Bb-F-C-G-D-A-E on a harpsichord. Raise the B-F#-C# with less than 1/4 comma tempering, or even (for the sake of demonstration) make them wider than pure, if you wish. Fit Eb and Ab/G# into place as wide 5ths, descending from Bb. Play all of the following spots: bars 47 and 86 of "La Poule", bar 30 of "Les Triolets", and bars 34 and 38 of "Les Sauvages", all from the G major and G minor pieces of c1728. Then, turn the page and play all of "L'enharmonique" as well. Turn back to "La Triomphante" and play through it, especially through the last couplet where Rameau's preface emphasized the use of B# and C simultaneously, and where he composed the C# major triad in the bar before that. 1/4 comma is too extreme for this music, especially when it runs into F# and Bb together, and when we encounter C# major on a downbeat.

Electronic device instructions for the Bach

Jon-O Addleman has generated a set of electronic pitches to match for this temperament, at A=415. I have not tried them myself, lacking a portable player to put next to the harpsichord (and preferring to work by ear anyway...). He has created recorded pitches for other temperaments also.

Instructions for PitchLab and ClearTune tuning apps are on the main page, in this section.

Return...