| I stumbled onto
fractional calculus my sophomore year of Undergrad during a
differential equations class lecture. Distracted by the thought, I
simply asked myself what would an equation look like that allowed for
taking nth derivatives of some function. My first derivation was taking
the nth derivative of polynomials and later I worked on cyclic
functions. After deriving these equations, I wondered if they were
valid for all n - even fractional values. It turns out that they are!
Most recently, I have have
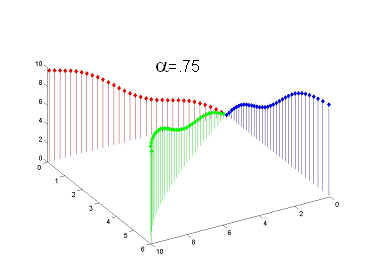
been studying a publication by Igor Podlubny. In the publication, he
deals with geometric
and physical interpretations of fractional integrals and below is
an example
of a geometrical interpretation of the Right Hand Riemann Liouville
Fractional
Integral for alpha = 0.75 (where alpha denotes the order of integration
- to see
the values of the axis examine figure 1 in the above link). To see
an
animation of varying alpha that I constructed click
here.
This work has now been
published. Please see "Geometrical
interpretation of fractional integration: shadows on the walls"
on JOMA.
Animation >> Geometric
Interpretation of a Fractional Integral
|

