|
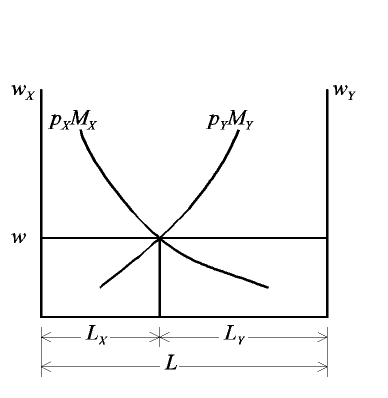
A rise in the price of either good shifts its sector's labor demand curve proportionally upward. This causes its intersection with the unchanged labor demand curve of the other sector to move up along that curve, increasing both the equilibrium common wage and employment in the sector where the price has risen.
Implicit in this is that output rises in the sector with the higher price and falls in the other sector. Also, since the wage rises by less than the upward shift of the curve (the heavy arrow in the figure, showing the size of the price increase), it follows that the nominal wage of labor rises relative to the unchanged price but falls relative to the increased price, implying that the effect on the real wage is, from this information, ambiguous.
Also implicit in the figure are the effects on real returns to specific factors, which respond to changes in labor employment by rising in the expanding sector and falling in the contracting sector.
|
|
An increase in the endowment of a specific factor in a sector makes labor in that sector more productive. Assuming constant returns to scale, the marginal product of labor depends only on the ratio of factors, and therefore the marginal product curve shifts horizontally by the percentage change in the specific factor, as shown. Like the price increases above, this raises the equilibrium employment in the sector with more of the specific factor, and raises the equilibrium nominal wage in both.
Output rises in the expanding sector, due now to the increases in both factors, while output in the other sector contracts. Since prices in this case are fixed, the rise in nominal wage is also an increase in real terms.
The real return to the non-expanded specific factor goes up, since it depends on its ratio to employed labor. The real return to the expanded specific factor goes down, analogously, since employment of labor in that sector expands by less than the increase in the specific factor (shown again by the heavy arrow in the figure).
|